Question

【题目】在平面直角坐标系xOy中，点满足方程.

（1）求点M的轨迹C的方程；

（2）作曲线C关于轴对称的曲线，记为，在曲线C上任取一点，过点P作曲线C的切线l，若切线l与曲线交于A，B两点，过点A，B分别作曲线的切线，证明的交点必在曲线C上.

Answer 1

【答案】（1）；（2）证明见解析.

【解析】

（1）将方程两边平方化简即得解；

（2）求出曲线在处的切线方程，联立直线与抛物线方程，消去，列出韦达定理，设，，分别求出曲线上在，两点处的切线，的方程，求出，的交点，即可得证.

（1）由，

两边平方并化简，得，

即，

所以点M的轨迹C的方程为.

（2）由（1）及题意可知曲线：，

又由知，

所以点处的切线方程为，

即，

又因为点在曲线C上，

所以，

所以切线方程为，

联立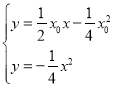消去整理得，，

设，，

所以，，（*）

又由，得，

所以曲线上点处的切线的方程为，

即，

同理可知，曲线上点处的切线的方程为，

联立方程组，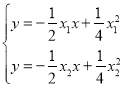

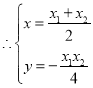
又由（*）式得，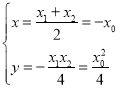

所以，的交点为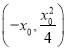，此点在曲线C上，

故，的交点必在曲线C上.