题目内容
在直角坐标系xoy中，设倾斜角为α的直线
（t为参数）与曲线 
（θ为参数）相交于不同两点A，B．（1）若
，求线段AB中点M的坐标；（2）若|PA|•|PB|=|OP|2，其中
，求直线l的斜率．
【答案】分析：（1）把直线和圆的参数方程化为普通方程，联立后根据根与系数的关系求出两交点中点的横坐标，待入直线方程再求中点的纵坐标；
（2）把直线方程和圆的方程联立，化为关于t的一元二次方程，运用直线参数方程中参数t的几何意义，结合给出的等式求解直线的倾斜角的正切值，则斜率可求，
解答：解：（1）当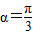
时，由
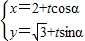，得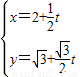
，所以直线方程为
，
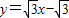由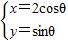
，得曲线C的普通方程为
，
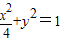设A（x1，y1），B（x2，y2）再由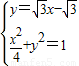
，得：13x2-24x+8=0，
所以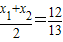
，
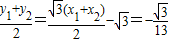，所以M的坐标为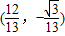
（2）把直线的参数方程代入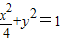
，得：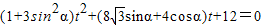
，
所以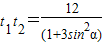
，由|PA|•|PB|=|t1t2|=|OP|2=7，得：
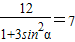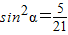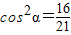，所以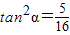
，
，
所以
，所以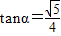
．
所以直线L的斜率为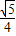
．
点评：本题考查了参数方程化普通方程，考查了直线的斜率、直线与椭圆的位置关系，解答此题（2）的关键是灵活运用直线参数方程中参数的几何意义，是中档题．
（2）把直线方程和圆的方程联立，化为关于t的一元二次方程，运用直线参数方程中参数t的几何意义，结合给出的等式求解直线的倾斜角的正切值，则斜率可求，
解答：解：（1）当
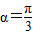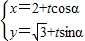时，由，得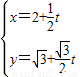，所以直线方程为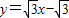，由
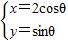，得曲线C的普通方程为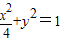，设A（x1，y1），B（x2，y2）再由
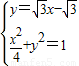，得：13x2-24x+8=0，所以
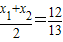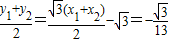，，所以M的坐标为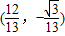（2）把直线的参数方程代入
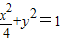，得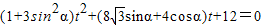：，所以
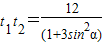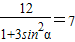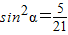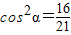，由|PA|•|PB|=|t1t2|=|OP|2=7，得：，所以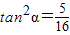，，所以
，所以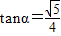．所以直线L的斜率为
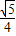．点评：本题考查了参数方程化普通方程，考查了直线的斜率、直线与椭圆的位置关系，解答此题（2）的关键是灵活运用直线参数方程中参数的几何意义，是中档题．
练习册系列答案
相关题目
如图所示，在直角坐标系xOy中，射线OA在第一象限，且与x轴的正半轴成定角60°，动点P在射线OA上运动，动点Q在y轴的正半轴上运动，△POQ的面积为