题目内容
如图,已知a∥b∥c,直线d与a、b、c相交于A、B、C三点.求证:a、b、c、d四线共面.
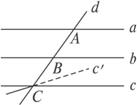
证法一:∵a∥b,∴由a、b可确定一个平面α,而A∈a,a
α,故A∈α.同理,B∈α.
故直线AB
α,即d
α.
又b∥c,故由b、c可确定平面β,
而B∈β,C∈β,
∴直线BC
β,即d
β.
这样相交直线b、d既在α内又在β内.
从而α与β重合,∴a、b、c、d四线共面.
证法二:∵a∥b,∴a、b可确定平面α.
又A∈α,B∈α,∴直线AB
α,即d
α.
假设c
α.∵C∈α,∴c∩α=C.
过C点作直线c′∥a,
又a∥c,∴c∥c′.
这与c∩c′=C相矛盾.
∴直线c
α.∴直线a、b、c、d四线共面.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
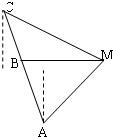如图，已知A、B、C是一条直路上的三点，AB与BC各等于1千米，从三点分别遥望塔M，在A处看见塔在北偏东45方向，在B处看见塔在正东方向，在C处看见塔在南偏东60°方向，求塔到直路ABC的最短距离．
如图，已知A、B、C、D四点共圆，延长AD和BC相交于点E，AB=AC．
如图，已知A、B、C是长轴为4的椭圆上的三点，点A是长轴的右顶点，BC过椭圆中心O，且
、
、
，如果AB＝BC＝1，
＝
，则
＝________．