Question

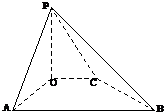（2008•卢湾区一模）（文） 已知四边形OABC为直角梯形，∠AOC=∠OAB=90°，PO⊥平面AC，且OA=3，AB=6，OC=2，PO=3．
（1）求证：AB⊥PA；
（2）求异面直线PB与OA所成的角θ（用反三角函数值表示）．

Answer 1

分析：（1）以O的坐标原点，OA，OC，OP方向分别为x，y，z轴正方向建立空间坐标系，分别求出AB与PA的方向向量的坐标，根据两向量的数量积为0，即可判断出AB⊥PA；
（2）分别求出异面直线PB与OA的方向向量的坐标，代入向量夹角公式，求出θ的余弦值，进而得到异面直线PB与OA所成的角θ．

解答：证明：（1）以O的坐标原点，OA，OC，OP方向分别为x，y，z轴正方向建立空间坐标系
∵OA=3，AB=6，OC=2，PO=3
∴A（3，0，0），B（3，6，0），P（0，0，3）
∴

AB

=（0，6，0），

PA

=（3，0，-3）
∵

AB

•

PA

=0
∴

AB

⊥

PA

即AB⊥PA；
解：（2）∵

PB

=（3，6，-3），

OA

=（3，0，0），
则异面直线PB与OA所成的角θ满足
cosθ=

| PB • OA |

| PB |•| OA |

=

9

3 6 •3

=

6

6

∴θ=arccos

6

6

．

点评：本题考查的知识点是异面直线及其所成的角，空间中直线与直线之间的位置关系，其中建立空间坐标系，将线面垂直问题及线线夹角问题转化为向量垂直及向量夹角问题是解答的关键．