题目内容
(2008•卢湾区一模)在△ABC中,已知∠A=45°,∠B=75°,点D在AB上,且CD=10.
(1)若点D与点A重合,试求线段AB的长;
(2)在下列各题中,任选一题,并写出计算过程,求出结果.
①(解答本题,最多可得6分)若CD⊥AB,求线段AB的长;
②(解答本题,最多可得8分)若CD平分∠ACB,求线段AB的长;
③(解答本题,最多可得10分)若点D为线段AB的中点,求线段AB的长.
(1)若点D与点A重合,试求线段AB的长;
(2)在下列各题中,任选一题,并写出计算过程,求出结果.
①(解答本题,最多可得6分)若CD⊥AB,求线段AB的长;
②(解答本题,最多可得8分)若CD平分∠ACB,求线段AB的长;
③(解答本题,最多可得10分)若点D为线段AB的中点,求线段AB的长.
分析:(1)先由A和B的度数求出C的度数,若点D与点A重合,DC即为AC的长,故由AC,sinB及sinC的值,利用正弦定理即可求出AB的长;
(2)若选①,由A和B的度数求出∠ACB的度数,根据CD与AB垂直,由A的度数求出∠ACD的度数,进而得到∠BCD的度数,在直角三角形ACD中,由CD的长及tan∠ACD的值,求出AD的长,在直角三角形BCD中,由tan∠BCD及CD的长,求出BD的长,利用AD+DB即可求出AB的长;
若选②,由A和B的度数求出∠ACB的度数,根据CD为角平分线,可得∠ACD=∠BCD=
∠ACB,在三角形ACD中,由CD,sinA及sin∠ACD的值,利用正弦定理求出AD的长,同理在三角形BCD中,由CD,sinB及sin∠BCD的值,利用正弦定理求出BD的长,根据AD+DB=AB,即可求出AB的长;
若选③,延长CD到E,使ED=CD,连接AE及BE,由D为AB中点,根据对角线互相平方的四边形为平行四边形可得ACBE为平行四边形,得到两组对边相等,在三角形ACE中,根据余弦定理表示出CE2=AC2+AE2-2AC•AE•cos∠CAE,且由AE与CB平行,根据∠ACB的度数求出∠CAE的度数,BC=AE,同时根据正弦定理,用sinB,sin∠ACB及AB表示出AE积AC,代入表示出的式子中,得到关于AB的方程,求出方程的解得到AB的长.
(2)若选①,由A和B的度数求出∠ACB的度数,根据CD与AB垂直,由A的度数求出∠ACD的度数,进而得到∠BCD的度数,在直角三角形ACD中,由CD的长及tan∠ACD的值,求出AD的长,在直角三角形BCD中,由tan∠BCD及CD的长,求出BD的长,利用AD+DB即可求出AB的长;
若选②,由A和B的度数求出∠ACB的度数,根据CD为角平分线,可得∠ACD=∠BCD=
| 1 |
| 2 |
若选③,延长CD到E,使ED=CD,连接AE及BE,由D为AB中点,根据对角线互相平方的四边形为平行四边形可得ACBE为平行四边形,得到两组对边相等,在三角形ACE中,根据余弦定理表示出CE2=AC2+AE2-2AC•AE•cos∠CAE,且由AE与CB平行,根据∠ACB的度数求出∠CAE的度数,BC=AE,同时根据正弦定理,用sinB,sin∠ACB及AB表示出AE积AC,代入表示出的式子中,得到关于AB的方程,求出方程的解得到AB的长.
解答:解:(1)∵∠A=45°,∠B=75°,
∴∠ACB=60°,又sin75° =sin(45° +30° )=
,
由正弦定理,得AB=
=
=15
-5
;
(2)根据题意画出相应的图形,如图所示:
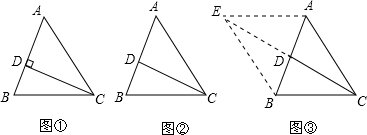
若选①,如图①所示:
若CD⊥AB,∠ACD=∠ACB-∠BCD=60°-15°=45°,又∠A=45°,
∴∠ACD=∠A,
∴AD=CD=10,又∠BCD=15°,由cos15°=sin75° =
,
得sin15° =
,tan15° =2-
,
故BD=10tan∠BCD=20-10
,AB=AD+DB=30-10
;
若选②,如图②所示:
∵∠A=45°,∠B=75°,
∴∠ACB=60°,又CD为角平分线,
∴∠ACD=∠BCD=30°,得AD=
=5
,BD=
=5(
-
),AB=AD+DB=5
;
若选③,根据正弦定理得:AC=
=
,BC=
=
,
如图③所示:延长CD到E,使DE=CD,连接EA、EB,
由余弦定理可得CE2=AC2+AE2-2AC•AE•cos∠CAE,
又cos∠CAE=cos(π-∠ACB)=-cos∠ACB,BC=AE,
得(2CD)2+AB2=2AC2+2BC2,
即400+AB2=
+
,
解得:AB=
.
∴∠ACB=60°,又sin75° =sin(45° +30° )=
| ||||
| 4 |
由正弦定理,得AB=
| AC•sin∠ACB |
| sin∠B |
| 10sin60° |
| sin75° |
| 2 |
| 6 |
(2)根据题意画出相应的图形,如图所示:

若选①,如图①所示:
若CD⊥AB,∠ACD=∠ACB-∠BCD=60°-15°=45°,又∠A=45°,
∴∠ACD=∠A,
∴AD=CD=10,又∠BCD=15°,由cos15°=sin75° =
| ||||
| 4 |
得sin15° =
| ||||
| 4 |
| 3 |
故BD=10tan∠BCD=20-10
| 3 |
| 3 |
若选②,如图②所示:
∵∠A=45°,∠B=75°,
∴∠ACB=60°,又CD为角平分线,
∴∠ACD=∠BCD=30°,得AD=
| 10sin∠ACD |
| sinA |
| 2 |
| 10sin∠BCD |
| sinB |
| 6 |
| 2 |
| 6 |
若选③,根据正弦定理得:AC=
| ABsinB |
| sin∠ACB |
| ABsin75° |
| sin60° |
| ABsinA |
| sin∠ACB |
| ABsin45° |
| sin60° |
如图③所示:延长CD到E,使DE=CD,连接EA、EB,
由余弦定理可得CE2=AC2+AE2-2AC•AE•cos∠CAE,
又cos∠CAE=cos(π-∠ACB)=-cos∠ACB,BC=AE,
得(2CD)2+AB2=2AC2+2BC2,
即400+AB2=
AB2(
| ||||
| 2•3 |
| 4AB2 |
| 3 |
解得:AB=
|
点评:此题考查了正弦定理,余弦定理,诱导公式,两角和与差的正弦函数公式,锐角三角形函数定义及特殊角的三角函数值,第二问是多选一的问题,学生只需选择一个解答即可.正弦、余弦定理很好的建立了三角形的边角关系,熟练掌握定理是解本题的关键.

练习册系列答案
相关题目