题目内容
【题目】在数列{an}中,a1=3,且对任意的正整数n,都有an+1=λan+2×3n,其中常数λ>0.
(1)设bn![]() .当λ=3时,求数列{bn}的通项公式;
.当λ=3时,求数列{bn}的通项公式;
(2)若λ≠1且λ≠3,设cn=an![]() ,证明:数列{cn}为等比数列;
,证明:数列{cn}为等比数列;
(3)当λ=4时,对任意的n∈N*,都有an≥M,求实数M的最大值.
【答案】(1)![]() ;(2)证明见解析(3)最大值为3.
;(2)证明见解析(3)最大值为3.
【解析】
(1)当![]() 可得
可得![]() ,等式两边同除
,等式两边同除![]() ,进而根据等差数列定义以及通项公式求解即可;
,进而根据等差数列定义以及通项公式求解即可;
(2)将![]() 代入
代入![]() 中,整理后得递推关系,再根据等比数列定义即可证明;
中,整理后得递推关系,再根据等比数列定义即可证明;
(3)当![]() 时可得
时可得![]() ,等式两边同除
,等式两边同除![]() 并设
并设![]() ,则
,则![]() ,利用累加法求得
,利用累加法求得![]() ,即可求得
,即可求得![]() ,再判断数列
,再判断数列![]() 的单调性,进而求解即可.
的单调性,进而求解即可.
(1)当λ=3时,有an+1=3an+2×3n,
∴![]() ,
,
![]()
![]() ,则
,则![]() ,
,
又∵![]() ,∴数列{bn}是首相为1,公差为
,∴数列{bn}是首相为1,公差为![]() 的等差数列,
的等差数列,
∴![]()
(2)证明:当λ>0且λ≠1且λ≠3时,
![]()
![]() ,
,
又∵![]() ,
,
∴数列![]() 是首项为
是首项为![]() ,公比为λ的等比数列
,公比为λ的等比数列
(3)当λ=4时,an+1=4an+2×3n,
∴![]() ,
,
设pn![]() ,∴
,∴![]() ,
,
∴![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
∴![]() ,
,
以上各式累加得: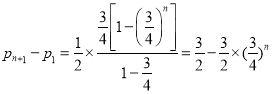 ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
![]()
![]() ,显然数列{an}是递增数列,
,显然数列{an}是递增数列,
∴最小项为a1=3,
∵对任意的n∈N*,都有an≥M,∴a1≥M,即M≤3,
∴实数M的最大值为3.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案
相关题目