题目内容
设a,b∈(0,+∞)且
证明:①n=1时,原不等式显然成立;
②设n=k时原不等式成立,
即(a+b)k-ak-bk≥22k-2k+1,
则n=k+1时,(a+b)k+1-ak+1-bk+1
=(a+b)[(a+b)k-ak-bk]+abk+akb≥(a+b)(22k-2k+1)+abk+akb,
由1=![]() ≥
≥![]() ,可得ab≥4,a+b≥
,可得ab≥4,a+b≥![]() ≥4.
≥4.
∴abk+akb≥2![]() =2k+2.
=2k+2.
∴(a+b)k+1-ak+1-bk+1≥(a+b)(22k-2k+1)+abk+akb≥4(22k-2k+1)+2k+2=22(k+1)-2(k+1)+1,
即n=k+1时原不等式成立.
由①②可知对于任何n∈N*原不等式成立.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
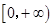 上的减函数,设a+b≤0,给出下列不等式:
上的减函数,设a+b≤0,给出下列不等式: