题目内容
已知a、b是两个非零向量，且｜a｜=｜b｜=｜a-b｜，则a与a+b的夹角为_______．
答案：30°
?解析：设a与a+b的夹角为θ，由｜a｜=｜b｜，得｜a｜2=｜b｜2.又由｜b｜2=｜a-b｜2=｜a｜2-2a·b+｜b｜2，∴ a·b=
｜a｜2.而｜a+b｜2=｜a｜2+2a·b+｜b｜2=3｜a｜2，∴｜a+b｜=
｜a｜.∴ cosθ=
=
=
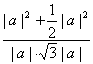.∵0°≤θ≤180°，∴θ=30°.
练习册系列答案
相关题目
已知
，
是两个非零向量，给定命题p：|
+
|=|
|+|
|；命题q：?t∈R，使得
=t
；则p是q的（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A、充分条件 |
| B、必要条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知
、
是两个非零向量，且|
|=|
|=|
-
|，则
与
+
的夹角为（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| a |
| b |
| A、30° | B、60° |
| C、90° | D、150° |