题目内容
【题目】已知函数![]()
若![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
若![]() ,则当
,则当![]() 时,函数
时,函数![]() 的图像是否总存在直线
的图像是否总存在直线![]() 上方?请写出判断过程.
上方?请写出判断过程.
【答案】(1) 在![]() 上单调递增;在
上单调递增;在![]() 上单调递减. (2)见解析
上单调递减. (2)见解析
【解析】试题分析:(1)先求函数导数,再求导函数零点,列表分析导函数符号变化规律,进而确定单调区间(2)先利用导数确定函数![]() 在
在![]() 上的单调性: 在
上的单调性: 在![]() 递增,在
递增,在![]() 递减,得最小值为
递减,得最小值为![]() ,再转化求证
,再转化求证![]() ,构造函数
,构造函数![]() ,利用导数易得函数
,利用导数易得函数![]() 先减后增,其最小值大于零
先减后增,其最小值大于零
试题解析:解:(1)函数定义域为![]() ,
, ![]()
则![]() 即
即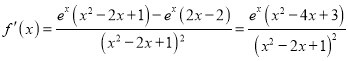
令![]() 时
时![]() ,
,
则当![]() 和
和![]() 时
时![]()
当![]() 时
时![]()
所以函数![]() 在
在![]() 上单调递增;在
上单调递增;在![]() 上单调递减.
上单调递减.
(2)由已知得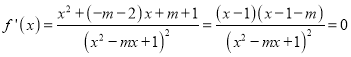 ,则
,则![]()
当![]() 时,
时, ![]() 在
在![]() 递增,在
递增,在![]() 递减,令
递减,令![]() ,
,
当![]() 时,
时, ![]() ,
, ![]() ,
,
∴函数![]() 图象在
图象在![]() 图象上方;
图象上方;
当![]() 时,函数
时,函数![]() 单调递减,
单调递减,
∴其最小值为![]() ,
, ![]() 最大值为m+1,
最大值为m+1,
∴下面判断![]() 与m+1的大小,
与m+1的大小,
即判断![]() 与
与![]() 的大小,其中
的大小,其中![]() ,
,
令![]() ,
, ![]() ,
,
令![]() ,则
,则![]() ,
,
∵![]() ,所以
,所以![]() ,
, ![]() 单调递增;
单调递增;
∴![]() ,
,![]()
![]() ,
,
故存在![]() 使得
使得![]() ,
,
∴![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增
上单调递增
∴![]() ,
,
∴![]() 时,
时, ![]() ,
,
即![]() 也即
也即![]() ,
,
∴函数![]() 的图象总在直线
的图象总在直线![]() 上方.
上方.

练习册系列答案
相关题目