题目内容
已知F1、F2是双曲线
-
=1(a>0,b>0)的左、右焦点,若在双曲线上的点P满足∠F1PF2=60°,且|OP|=
a(O为坐标原点),则该双曲线的离心率是( )
| x2 |
| a2 |
| y2 |
| b2 |
| 7 |
分析:假设|F1P|=x,分别根据中线定理和余弦定理建立等式求得c2+5a2=14a2-2c2,可得a和c的关系,即可求双曲线的离心率.
解答:解:不妨设P在左支上,|F1P|=x,则|F2P|=2a+x
∵OP为三角形F1F2P的中线,∴根据三角形中线定理可知x2+(2a+x)2=2(c2+7a2)
整理得x(x+2a)=c2+5a2
由余弦定理可知x2+(2a+x)2-x(2a+x)=4c2
整理得x(x+2a)=14a2-2c2
进而可知c2+5a2=14a2-2c2
∴3a2=c2
∴e=
=
故选C.
∵OP为三角形F1F2P的中线,∴根据三角形中线定理可知x2+(2a+x)2=2(c2+7a2)
整理得x(x+2a)=c2+5a2
由余弦定理可知x2+(2a+x)2-x(2a+x)=4c2
整理得x(x+2a)=14a2-2c2
进而可知c2+5a2=14a2-2c2
∴3a2=c2
∴e=
| c |
| a |
| 3 |
故选C.
点评:本题考查了双曲线的定义、标准方程,考查余弦定理的运用,考查学生的计算能力,属于中档题.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
已知F1,F2分别为双曲
-
=1(a>0,b>0)的左、右焦点,P为双曲线左支上任一点,若
的最小值为8a,则双曲线的离心率e的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
| |PF2|2 |
| |PF1| |
| A、(1,+∞) |
| B、(0,3] |
| C、(1,3] |
| D、(0,2] |
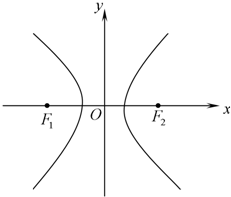
 的左、右两个焦点,点P是双曲线上一点,且|PF1|.|PF2|=32,求∠F1PF2的大小.
的左、右两个焦点,点P是双曲线上一点,且|PF1|.|PF2|=32,求∠F1PF2的大小.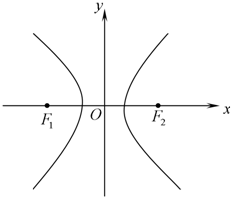
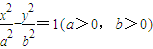 的左、右焦点,P为双曲线左支上任一点,若
的左、右焦点,P为双曲线左支上任一点,若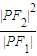 的最小值为8a,则双曲线的离心率e的取值范围是( )
的最小值为8a,则双曲线的离心率e的取值范围是( )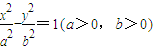 的左、右焦点,P为双曲线左支上任一点,若
的左、右焦点,P为双曲线左支上任一点,若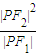 的最小值为8a,则双曲线的离心率e的取值范围是( )
的最小值为8a,则双曲线的离心率e的取值范围是( )