题目内容
已知x,y,z为实数,且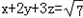 ,
,
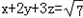 ,
, (1)求x2+y2+z2的最小值;
(2)设|2t﹣1|=x2+y2+z2,求实数t的取值范围.
(2)设|2t﹣1|=x2+y2+z2,求实数t的取值范围.
解:(1)由柯西不等式(12+22+32)(x2+y2+z2)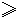 (1
(1 x+2
x+2 y+3
y+3 z)2
z)2
得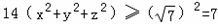 ,
,
所以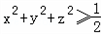 ,
,
当且仅当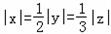 时取等号,即x2+y2+z2的最小值为
时取等号,即x2+y2+z2的最小值为
(2)由(1)得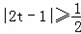 ,则
,则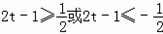 ,
,
解得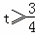 或
或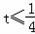 ,
,
t的取值范围是
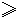 (1
(1 x+2
x+2 y+3
y+3 z)2
z)2得
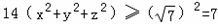 ,
,所以
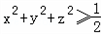 ,
,当且仅当
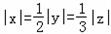 时取等号,即x2+y2+z2的最小值为
时取等号,即x2+y2+z2的最小值为
(2)由(1)得
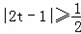 ,则
,则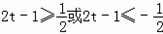 ,
,解得
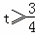 或
或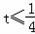 ,
,t的取值范围是


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
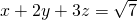 ,
,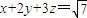 ,
,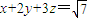 ,
,