题目内容
选修4-5:不等式选讲已知x,y,z为实数,且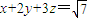 ,
,(Ⅰ)求x2+y2+z2的最小值;
(Ⅱ)设|2t-1|=x2+y2+z2,求实数t的取值范围.
【答案】分析:(I)利用题中条件:“ ”构造柯西不等式(12+22+32)(x2+y2+z2)≥(1•x+2•y+3•z)2这个条件进行计算即可.
”构造柯西不等式(12+22+32)(x2+y2+z2)≥(1•x+2•y+3•z)2这个条件进行计算即可.
(II)由(Ⅰ)得 ,解此绝对值不等式即可得到实数t的取值范围.
,解此绝对值不等式即可得到实数t的取值范围.
解答:解:(Ⅰ)由柯西不等式(12+22+32)(x2+y2+z2)≥(1•x+2•y+3•z)2
得 ,所以
,所以 ,
,
当且仅当 时取等号,即x2+y2+z2的最小值为
时取等号,即x2+y2+z2的最小值为 …(3分)
…(3分)
(Ⅱ)由(Ⅰ)得 ,则
,则 ,解得
,解得 或
或 ,
,
即实数t的取值范围是 …(7分)
…(7分)
点评:本题考查用综合法证明不等式,关键是利用:(12+22+32)(x2+y2+z2)≥(1•x+2•y+3•z)2这个不等关系,还考查了绝对值不等式的解法.
 ”构造柯西不等式(12+22+32)(x2+y2+z2)≥(1•x+2•y+3•z)2这个条件进行计算即可.
”构造柯西不等式(12+22+32)(x2+y2+z2)≥(1•x+2•y+3•z)2这个条件进行计算即可.(II)由(Ⅰ)得
 ,解此绝对值不等式即可得到实数t的取值范围.
,解此绝对值不等式即可得到实数t的取值范围.解答:解:(Ⅰ)由柯西不等式(12+22+32)(x2+y2+z2)≥(1•x+2•y+3•z)2
得
 ,所以
,所以 ,
,当且仅当
 时取等号,即x2+y2+z2的最小值为
时取等号,即x2+y2+z2的最小值为 …(3分)
…(3分)(Ⅱ)由(Ⅰ)得
 ,则
,则 ,解得
,解得 或
或 ,
,即实数t的取值范围是
 …(7分)
…(7分)点评:本题考查用综合法证明不等式,关键是利用:(12+22+32)(x2+y2+z2)≥(1•x+2•y+3•z)2这个不等关系,还考查了绝对值不等式的解法.

练习册系列答案
 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目