题目内容
(2012•宣城模拟)已知数列{an}的前n项和为Sn,对任意n∈N*,有2an=Sn+n.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设f(n)=n2 (n∈N*),试比较Sn与f(n)的大小,并说明理由.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设f(n)=n2 (n∈N*),试比较Sn与f(n)的大小,并说明理由.
分析:(Ⅰ)通过已知条件构造新数列,求出新数列的通项公式,然后求数列{an}的通项公式;
(Ⅱ)求出Sn,通过比较n=1,2,比较Sn与f(n)的大小,猜想n≥3时的结果,利用二项式定理证明即可.
(Ⅱ)求出Sn,通过比较n=1,2,比较Sn与f(n)的大小,猜想n≥3时的结果,利用二项式定理证明即可.
解答:解:(Ⅰ)当n=1时,2a1=a1+1∴a1=1…(1分)
∵2an=Sn+n,n∈N*,∴2an-1=Sn-1+n-1,n≥2,
两式相减得an=2an-1+1,n≥2,即an+1=2(an-1+1),n≥2,
令bn=an+1,则
=2,n≥2且b1=a1+1=2,
所以bn=b1•2n-1=2×2n-1=2n.n∈N*,
∴an=2n-1,n∈N*…(7分)
(Ⅱ)由(Ⅰ)an=2n-1,n∈N*,
得Sn=(2+22+23+…+2n)-n
=
-n
=2n+1-n-2
当n=1,2时,Sn=f(n);当n≥3时,Sn>f(n)…(9分)
只需证2n+1>n2+n+2,n≥3,
利用(1+1)2=
+
+
+…+
>
+
+
=
(n2+n+2).
∴2n+1>n2+n+2,n≥3.…(13分)
∵2an=Sn+n,n∈N*,∴2an-1=Sn-1+n-1,n≥2,
两式相减得an=2an-1+1,n≥2,即an+1=2(an-1+1),n≥2,
令bn=an+1,则
| bn |
| bn-1 |
所以bn=b1•2n-1=2×2n-1=2n.n∈N*,
∴an=2n-1,n∈N*…(7分)
(Ⅱ)由(Ⅰ)an=2n-1,n∈N*,
得Sn=(2+22+23+…+2n)-n
=
| 2(1-2n+1) |
| 1-2 |
=2n+1-n-2
当n=1,2时,Sn=f(n);当n≥3时,Sn>f(n)…(9分)
只需证2n+1>n2+n+2,n≥3,
利用(1+1)2=
| C | 0 n |
| C | 1 n |
| C | 2 n |
| C | n n |
| C | 0 n |
| C | 1 n |
| C | 2 n |
| 1 |
| 2 |
∴2n+1>n2+n+2,n≥3.…(13分)
点评:本题考查数列通项公式的求法,二项式定理证明不等式的应用,考查计算能力,转化思想;也可用数学归纳法证,也可构造函数s(x)=2x+1,f(x)=x2+x+2,利用导数证明,方法比较多.

练习册系列答案
相关题目
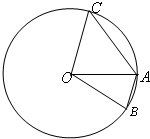 (2012•宣城模拟)如图,⊙O的半径为1,点A,B,C是⊙O上的点,且∠AOB=30°,AC=2AB,则
(2012•宣城模拟)如图,⊙O的半径为1,点A,B,C是⊙O上的点,且∠AOB=30°,AC=2AB,则