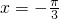题目内容
已知函数y=4cos2x+4 sinxcosx-2,x∈R.
sinxcosx-2,x∈R.
①求函数的周期;
②写出函数的单调增区间;
③当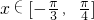 时,求函数的最大值.
时,求函数的最大值.
解:y=4cos2x+4 sinxcosx-2=
sinxcosx-2= =
=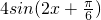
①函数的周期T= =π
=π
②当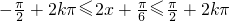
 为函数的单调增区间
为函数的单调增区间
③当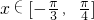 时,
时,
 时,函数的最大值为4.
时,函数的最大值为4.
分析:由已知中函数y=4cos2x+4 sinxcosx-2,根据二倍解公式,及辅助角公式,我们易将函数的解析式化为正弦型函数
sinxcosx-2,根据二倍解公式,及辅助角公式,我们易将函数的解析式化为正弦型函数
①根据函数的解析式,求出ω,代入T= ,即可求出函数的周期;
,即可求出函数的周期;
②根据正弦函数的单调性,构造不等式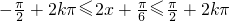 ,解不等式即可求出函数的单调增区间;
,解不等式即可求出函数的单调增区间;
③当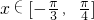 时,分析出相位角的范围,进而根据正弦型函数的性质得到函数的最大值.
时,分析出相位角的范围,进而根据正弦型函数的性质得到函数的最大值.
点评:本题考查的知识点是三角函数的恒等变换及化简求值,其中熟练掌握正弦型函数的参数与性质的关系是解答本题的关键.
 sinxcosx-2=
sinxcosx-2= =
=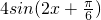
①函数的周期T=
 =π
=π②当
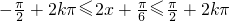
 为函数的单调增区间
为函数的单调增区间 ③当
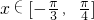 时,
时,
 时,函数的最大值为4.
时,函数的最大值为4.分析:由已知中函数y=4cos2x+4
 sinxcosx-2,根据二倍解公式,及辅助角公式,我们易将函数的解析式化为正弦型函数
sinxcosx-2,根据二倍解公式,及辅助角公式,我们易将函数的解析式化为正弦型函数①根据函数的解析式,求出ω,代入T=
 ,即可求出函数的周期;
,即可求出函数的周期;②根据正弦函数的单调性,构造不等式
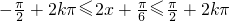 ,解不等式即可求出函数的单调增区间;
,解不等式即可求出函数的单调增区间;③当
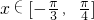 时,分析出相位角的范围,进而根据正弦型函数的性质得到函数的最大值.
时,分析出相位角的范围,进而根据正弦型函数的性质得到函数的最大值.点评:本题考查的知识点是三角函数的恒等变换及化简求值,其中熟练掌握正弦型函数的参数与性质的关系是解答本题的关键.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
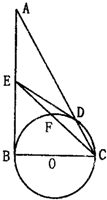 (选修4-1)如图,在△ABC中,∠ABC=90°,以BC为直径的圆O交AC于点D,设E为AB的中点.
(选修4-1)如图,在△ABC中,∠ABC=90°,以BC为直径的圆O交AC于点D,设E为AB的中点. 
 )的图象经过点(0,2),则不是该函数的一条对称轴方程为
)的图象经过点(0,2),则不是该函数的一条对称轴方程为