题目内容
一个口袋中有 个白球和
个白球和 个红球(
个红球( ,且
,且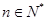 ),每次从袋中摸出两个球(每次摸球后把这两个球放回袋中),若摸出的两个球颜色相同为中奖,否则为不中奖.
),每次从袋中摸出两个球(每次摸球后把这两个球放回袋中),若摸出的两个球颜色相同为中奖,否则为不中奖.
(1)试用含 的代数式表示一次摸球中奖的概率
的代数式表示一次摸球中奖的概率 ;
;
(2)若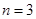 ,求三次摸球恰有一次中奖的概率;
,求三次摸球恰有一次中奖的概率;
(3)记三次摸球恰有一次中奖的概率为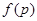 ,当
,当 为何值时,
为何值时,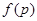 取最大值.
取最大值.
(1) ,(2)
,(2) ,(3)
,(3)  .
.
解析试题分析:(1)求古典概型概率,关键正确计算事件所包含的基本事件. 一次摸球从 个球中任选两个,有
个球中任选两个,有 种选法,其中两球颜色相同有
种选法,其中两球颜色相同有 种选法;因此一次摸球中奖的概率
种选法;因此一次摸球中奖的概率 .(2)因为每次摸球后把这两个球放回袋中,所以事件为独立重复试验. 由(1)得一次摸球中奖的概率是
.(2)因为每次摸球后把这两个球放回袋中,所以事件为独立重复试验. 由(1)得一次摸球中奖的概率是 ,所以三次摸球恰有一次中奖的概率是
,所以三次摸球恰有一次中奖的概率是 .(3)同(2)可得三次摸球中恰有一次中奖的概率是
.(3)同(2)可得三次摸球中恰有一次中奖的概率是 ,这是三次函数,利用导数求最值. 由
,这是三次函数,利用导数求最值. 由 知
知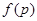 在
在 是增函数,在
是增函数,在 是减函数,所以当
是减函数,所以当 时,
时,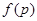 取最大值.
取最大值.
试题解析:(1)一次摸球从 个球中任选两个,有
个球中任选两个,有 种选法,
种选法,
其中两球颜色相同有 种选法;
种选法;
∴一次摸球中奖的概率 . 4分
. 4分
(2)若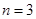 ,则一次摸球中奖的概率是
,则一次摸球中奖的概率是 ,三次摸球是独立重复实验,三次摸球中恰有一次中奖的概率是
,三次摸球是独立重复实验,三次摸球中恰有一次中奖的概率是 . 8分
. 8分
(3)设一次摸球中奖的概率是 ,
,
则三次摸球中恰有一次中奖的概率是 ,
,
∵ ,
,
∴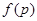 在
在 是增函数,在
是增函数,在 是减函数,
是减函数,
∴当 时,
时,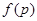 取最大值. 10分
取最大值. 10分
由 .
.
∴ 时,三次摸球中恰有一次中奖的概率最大. 12分
时,三次摸球中恰有一次中奖的概率最大. 12分
考点:古典概型概率,独立重复实验,利用导数求最值

 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案在某次体检中,有6位同学的平均体重为65公斤.用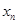 表示编号为
表示编号为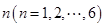 的同学的体重,且前5位同学的体重如下:
的同学的体重,且前5位同学的体重如下:
| 编号n | 1 | 2 | 3 | 4 | 5 |
| 体重xn | 60 | 66 | 62 | 60 | 62 |
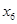 及这6位同学体重的标准差
及这6位同学体重的标准差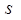 ;
;(2)从前5位同学中随机地选2位同学,求恰有1位同学的体重在区间
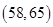 中的概率.
中的概率. 2013年9月20日是第25个全国爱牙日。某区卫生部门成立了调查小组,调查 “常吃零食与患龋齿的关系”,对该区六年级800名学生进行检查,按患龋齿和不患龋齿分类,得汇总数据:不常吃零食且不患龋齿的学生有60名,常吃零食但不患龋齿的学生有100名,不常吃零食但患龋齿的学生有140名.
(1)能否在犯错概率不超过0.001的前提下,认为该区学生的常吃零食与患龋齿有关系?
(2)4名区卫生部门的工作人员随机分成两组,每组2人,一组负责数据收集,另一组负责数据处理.求工作人员甲分到负责收集数据组,工作人员乙分到负责数据处理组的概率.
 | 0.010 | 0.005 | 0.001 |
 | 6.635 | 7.879 | 10.828 |

经调查发现,人们长期食用含高浓度甲基汞的鱼类会引起汞中毒,其中罗非鱼体内汞含量比其它鱼偏高.现从一批数量很大的罗非鱼中随机地抽出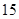 条作样本,经检测得各条鱼的汞含量的茎叶图(以小数点前的数字为茎,小数点后一位数字为叶)如下:
条作样本,经检测得各条鱼的汞含量的茎叶图(以小数点前的数字为茎,小数点后一位数字为叶)如下:
罗非鱼的汞含量(ppm)
 | 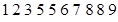 |
 | 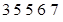 |
《中华人民共和国环境保护法》规定食品的汞含量不得超过
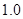 ppm.
ppm.(1)检查人员从这
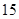 条鱼中,随机抽出
条鱼中,随机抽出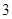 条,求
条,求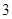 条中恰有
条中恰有 条汞含量超标的概率;
条汞含量超标的概率;(2)若从这批数量很大的鱼中任选
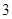 条鱼,记
条鱼,记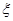 表示抽到的汞含量超标的鱼的条数.以此
表示抽到的汞含量超标的鱼的条数.以此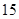 条鱼的样本数据来估计这批数量很大的鱼的总体数据,求
条鱼的样本数据来估计这批数量很大的鱼的总体数据,求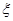 的分布列及数学期望
的分布列及数学期望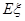 .
. 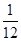 (i=1,2,…,12);设每售出一台电冰箱,电器商获利300元.如销售不出,则每台每月需花保管费100元.问电器商每月初购进多少台电冰箱才能使月平均收益最大?
(i=1,2,…,12);设每售出一台电冰箱,电器商获利300元.如销售不出,则每台每月需花保管费100元.问电器商每月初购进多少台电冰箱才能使月平均收益最大? 三个社区参加社会实践,要求每个社区至少有一名同学.
三个社区参加社会实践,要求每个社区至少有一名同学. 社区的概率;
社区的概率; 为四名同学中到
为四名同学中到 的值.
的值. 月
月 日至
日至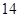 日的空气质量指数趋势图,空气质量指数(
日的空气质量指数趋势图,空气质量指数(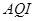 )小于
)小于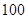 表示空气质量优良,空气质量指数大于
表示空气质量优良,空气质量指数大于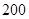 表示空气重度污染,某人随机选择
表示空气重度污染,某人随机选择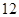 日中的某一天到达该市,并停留
日中的某一天到达该市,并停留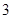 天.
天.
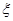 是此人停留期间空气重度污染的天数,求
是此人停留期间空气重度污染的天数,求