Question

已知△ABC中,∠ABC=30°,PA⊥平面ABC,PC⊥BC,PB与平面ABC成45°角.求二面角A-PB-C的正弦值.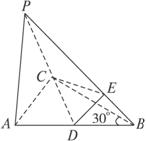

Answer 1

解析:过点C作CD⊥AB于点D,

∵PA⊥平面ABC,CD平面ABC,

∴CD⊥PA.∴CD⊥平面PAB.

作DE⊥PB于E,连结CE,则CE⊥PB.∴∠DEC为二面角A-PB-C的平面角.

设AC=m,由PC⊥BC,PA⊥平面ABC得∠ACB=90°.又∠ABC=30°,知BC=m.

∴CD=BCsin30°=m,AB==2m.

由PA⊥平面ABC,知∠PBA为PB与平面ABC所成的角.

∴∠PBA=45°.∴PA=BA=2m.

在Rt△PAC中,PC=.

在Rt△PBC中,PB=.

∵PB·EC=PC·BC,

∴EC=.

在Rt△ECD中,sin∠CED=,

即二面角APBC的正弦值为.

小结:此题作二面角的平面角的方法是:过二面角的面PBC内的点C向二面角的另一个面PAB作垂线CD,垂足为D,然后由D向二面角的棱PB作垂线,垂足为E,连结CE,由三垂线定理知CE⊥PB,从而∠DEC为二面角的平面角.此种作二面角的方法称为“垂线法”.“垂线法”是作二面角的平面角的常用方法,应当重视这种方法.此题也可过A作AG⊥PC于G(易证AG⊥平面PBC),利用AG作二面角A-PB-C的平面角.