题目内容
已知函数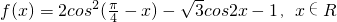 .
.
(1)求函数f(x)单调递增区间;
(2)若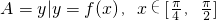 ,不等式|x-m|<3的解集为B,A∩B=A,求实数m的取值范围.
,不等式|x-m|<3的解集为B,A∩B=A,求实数m的取值范围.
解:(1) ,…(5分)
,…(5分)
由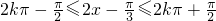 解得:
解得: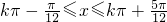 ,
,
∴f(x)在区间 上单调递增.…(8分)
上单调递增.…(8分)
(2)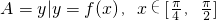 ,不等式|x-m|<3的解集为B,A∩B=A,
,不等式|x-m|<3的解集为B,A∩B=A,
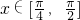 ,∴
,∴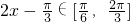 ,∴A=[1,2],
,∴A=[1,2],
又解得B=(m-3,m+3)…(12分)
而A∩B=A?A⊆B∴ ,得-1<m<4…(16分).
,得-1<m<4…(16分).
分析:(1)利用二倍角公式、诱导公式、两角差的正弦函数化简函数的表达式,通过正弦函数的单调增区间,求出函数的单调增区间.
(2)通过(1)根据x的范围求出集合A,利用A∩B=A,求出集合B,得到不等式组,求出m的范围即可.
点评:本题是中档题,考查三角函数的化简求值,二倍角公式两角差的正弦函数的应用,考查计算能力,转化思想.
 ,…(5分)
,…(5分)由
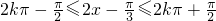 解得:
解得: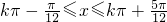 ,
,∴f(x)在区间
 上单调递增.…(8分)
上单调递增.…(8分)(2)
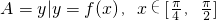 ,不等式|x-m|<3的解集为B,A∩B=A,
,不等式|x-m|<3的解集为B,A∩B=A,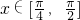 ,∴
,∴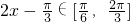 ,∴A=[1,2],
,∴A=[1,2],又解得B=(m-3,m+3)…(12分)
而A∩B=A?A⊆B∴
 ,得-1<m<4…(16分).
,得-1<m<4…(16分).分析:(1)利用二倍角公式、诱导公式、两角差的正弦函数化简函数的表达式,通过正弦函数的单调增区间,求出函数的单调增区间.
(2)通过(1)根据x的范围求出集合A,利用A∩B=A,求出集合B,得到不等式组,求出m的范围即可.
点评:本题是中档题,考查三角函数的化简求值,二倍角公式两角差的正弦函数的应用,考查计算能力,转化思想.

练习册系列答案
相关题目





 ,如果满足;对任意
,如果满足;对任意 ,存在常数
,存在常数 ,都有
,都有 成立,则称
成立,则称 ,
,
 时,求函数
时,求函数 上的值域,并判断函数
上的值域,并判断函数 上是以3为上界函数值,求实数
上是以3为上界函数值,求实数 的取值范围;
的取值范围; ,求函数
,求函数 在
在 上的上界T的取值范围。
上的上界T的取值范围。 .
. 上的函数值的取值范围.
上的函数值的取值范围. .
. 上的函数值的取值范围.
上的函数值的取值范围.