题目内容
如图,过四棱柱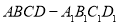 形木块上底面内的一点
形木块上底面内的一点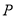 和下底面的对角线
和下底面的对角线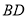 将木块锯开,得到截面
将木块锯开,得到截面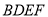 .
.
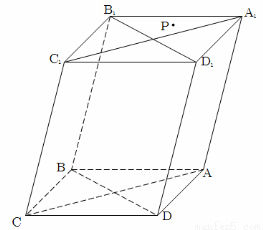
(1)请在木块的上表面作出过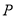 的锯线
的锯线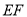 ,并说明理由;
,并说明理由;
(2)若该四棱柱的底面为菱形,四边形时矩形 ,试证明:平面
,试证明:平面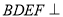 平面
平面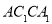 .
.
(1)如图 (2)详见解析
【解析】
试题分析:(1)本题实质为确定截面与上底面的交线,这利用面面平行性质定理,可得交线相互平行:即由平面ABCD//平面A1B1C1D1,平面BDFE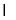 平面ABCD=BD,平面BDFE
平面ABCD=BD,平面BDFE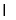 平面A1B1C1D1=EF,得EF//BD,又 B1B//D1D,从而EF// B1D1 (2)证明面面垂直,一般利用其判定定理,即证线面垂直:由BD
平面A1B1C1D1=EF,得EF//BD,又 B1B//D1D,从而EF// B1D1 (2)证明面面垂直,一般利用其判定定理,即证线面垂直:由BD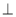 A1A,BD
A1A,BD AC得到BD
AC得到BD 平面A1C1CA,从而平面BDFE
平面A1C1CA,从而平面BDFE 平面A1C1CA
平面A1C1CA
试题解析:(1)
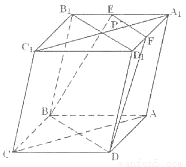
在上底面内过点P作B1D1的平行线分别交A1D1,A1B1于F,E两点,则EF为所作的锯线. 2分
在四棱柱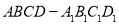 中,侧棱B1B//D1D,B1B=D1D,
中,侧棱B1B//D1D,B1B=D1D,
所以四边形BB1D1D是平行四边形,B1D1//BD 4分
又平面ABCD//平面A1B1C1D1,平面BDFE 平面ABCD=BD,平面BDFE
平面ABCD=BD,平面BDFE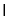 平面A1B1C1D1=EF,
平面A1B1C1D1=EF,
所以EF//BD,从而EF// B1D1 7分
(2) 证明:由于四边形BB1D1D是矩形,所以BD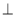 B1B,又A1A//B1B
B1B,又A1A//B1B
所以BD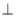 A1A 9分
A1A 9分
又四棱柱的底面为菱形,所以BD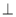 AC
AC
因为AC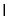 A1A=A,AC
A1A=A,AC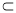 平面A1C1CA, A1A
平面A1C1CA, A1A 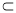 平面A1C1CA
平面A1C1CA
所以BD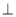 平面A1C1CA 12分
平面A1C1CA 12分
因为BD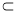 平面BDFE
平面BDFE
所以平面BDFE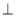 平面A1C1CA 14分
平面A1C1CA 14分
考点:面面平行性质定理,面面垂直判定定理

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 的部分图象如图所示,则在
的部分图象如图所示,则在 上,下列函数中与
上,下列函数中与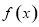 的单调性不同的是
的单调性不同的是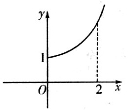
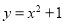 B.
B. 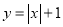
 D.
D. 
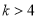 是方程
是方程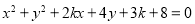 表示圆的充要条件;
表示圆的充要条件;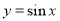 的图象向右平移
的图象向右平移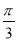 单位,再保持纵坐标不变,横坐标变为原来的
单位,再保持纵坐标不变,横坐标变为原来的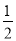 ,得到函数
,得到函数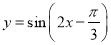 的图象;
的图象;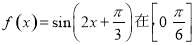 上为增函数;
上为增函数;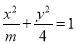 的焦距为2,则实数m的值等于5.
的焦距为2,则实数m的值等于5. 中,
中, 分别为
分别为 的中点,记三棱锥
的中点,记三棱锥 的体积为
的体积为 ,
, 的体积为
的体积为 ,则
,则
 满足
满足 ,则
,则 的模为
的模为  满足
满足 ,则
,则 的最大值为
的最大值为  为
为 
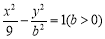 ,过其右焦点
,过其右焦点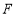 作圆
作圆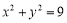 的两条切线,切点记作
的两条切线,切点记作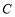 ,
,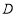 ,双曲线的右顶点为
,双曲线的右顶点为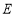 ,
,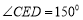 ,则其双曲线的离心率为( )
,则其双曲线的离心率为( )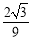 (B)
(B)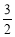 (C)
(C)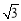 (D)
(D)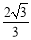
 与曲线
与曲线 恰有一个公共点,则
恰有一个公共点,则 的取值范围是
的取值范围是