题目内容
已知函数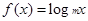 (
(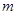 为常数,
为常数,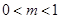 ),且数列
),且数列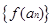 是首项为
是首项为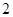 ,公差为
,公差为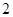 的等差数列.
的等差数列.
(1) 若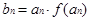 ,当
,当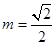 时,求数列
时,求数列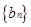 的前
的前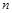 项和
项和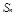 ;
;
(2)设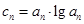 ,如果
,如果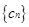 中的每一项恒小于它后面的项,求
中的每一项恒小于它后面的项,求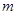 的取值范围.
的取值范围.
【答案】
(1)  (2)
(2) 
【解析】
试题分析:(1) 由题意 ,即
,即 , 1分
, 1分
 . ……2分
. ……2分
 ,
,
当 时,
时, .
3分
.
3分
∴ , ①
, ①
 ②
4分
②
4分
①-②,得
 6分
6分
∴ 7分
7分
(2)由(1)知, ,要使
,要使 对一切
对一切 成立,
成立,
即 对一切
对一切 成立. ……8分
成立. ……8分
 ,对一切
,对一切 恒成立,
恒成立,
只需 , 10分
, 10分
 单调递增,∴当
单调递增,∴当 时,
时, .
12分
.
12分
∴ ,且
,且 , ∴
, ∴ . 13分
. 13分
综上所述,存在实数 满足条件. 14分
满足条件. 14分
考点:本题考查了数列的求和及不等式的证明
点评:数列的通项公式及应用是数列的重点内容,数列的大题对逻辑推理能力有较高的要求,在数列中突出考查学生的理性思维,这是近几年新课标高考对数列考查的一个亮点,也是一种趋势.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目































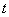




 (
( 为常数,
为常数, 且
且 )的图象过点
)的图象过点 .
. ,试判断函数
,试判断函数 的奇偶性,并说明理由.
的奇偶性,并说明理由.  (
( 为常数,
为常数, ),满足
),满足 ,且
,且 有两个相同的解。
有两个相同的解。 的表达式;
的表达式; 满足
满足 ,且
,且 ,求证:数列
,求证:数列 是等差数列。
是等差数列。 (
( 为常数),直线l与函数
为常数),直线l与函数 的图象都相切,且l与函数
的图象都相切,且l与函数 的图象的切点的横坐标为l.
的图象的切点的横坐标为l. 的解的个数.
的解的个数.