题目内容
两人约定在20:00到21:00之间相见(两人出发是各自独立,且在20:00到21:00各时刻相见的可能性是相等的),并且先到者必须等迟到者40分钟方可离去,则两人在约定时间内能相见的概率是
- A.

- B.

- C.

- D.

B
分析:由题意设事件A为“甲乙两人能会面”,求出试验包含的所有事件,并且事件对应的集合表示的面积是s=1,再求出满足条件的事件,并且得到事件对应的集合表示的面积是 ,进而根据几何概率模型的计算公式可得答案.
,进而根据几何概率模型的计算公式可得答案.
解答: 解:由题意知本题是一个几何概型,设事件A为“甲乙两人能会面”,
解:由题意知本题是一个几何概型,设事件A为“甲乙两人能会面”,
试验包含的所有事件是Ω={(x,y)|20<x<21,20<y<21},并且事件对应的集合表示的面积是s=1,
满足条件的事件是A={(x,y)|20<x<21,20<y<21,|x-y|<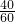 =
= }
}
所以事件对应的集合表示的面积是1-2× ×
× ×
× =
= ,
,
根据几何概型概率公式得到P= .
.
则两人在约定时间内能相见的概率是 .
.
故选B.
点评:解决此类问题的关键是熟练掌握几何概型的定义与概率计算公式,而几何概率模型一般通过事件的长度、面积或者体积之比来求事件发生的概率,因此只要根据题意判断出题目是属于那种类型即可,此题属于中档题,是根据面积之比来计算事件发生的概率.
分析:由题意设事件A为“甲乙两人能会面”,求出试验包含的所有事件,并且事件对应的集合表示的面积是s=1,再求出满足条件的事件,并且得到事件对应的集合表示的面积是
 ,进而根据几何概率模型的计算公式可得答案.
,进而根据几何概率模型的计算公式可得答案.解答:
 解:由题意知本题是一个几何概型,设事件A为“甲乙两人能会面”,
解:由题意知本题是一个几何概型,设事件A为“甲乙两人能会面”,试验包含的所有事件是Ω={(x,y)|20<x<21,20<y<21},并且事件对应的集合表示的面积是s=1,
满足条件的事件是A={(x,y)|20<x<21,20<y<21,|x-y|<
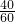 =
= }
}所以事件对应的集合表示的面积是1-2×
 ×
× ×
× =
= ,
,根据几何概型概率公式得到P=
 .
.则两人在约定时间内能相见的概率是
 .
.故选B.
点评:解决此类问题的关键是熟练掌握几何概型的定义与概率计算公式,而几何概率模型一般通过事件的长度、面积或者体积之比来求事件发生的概率,因此只要根据题意判断出题目是属于那种类型即可,此题属于中档题,是根据面积之比来计算事件发生的概率.

练习册系列答案
相关题目



