题目内容

选修4-4：坐标系与参数方程
在直角坐标系xOy中，曲线C₁的参数方程为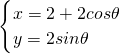 $数学公式$ 若曲线C₂与曲线C₁关于直线y=x对称
（Ⅰ）求曲线C₂的直角坐标方程；
（Ⅱ）在以O为极点，x轴的正半轴为极轴的极坐标系中，射线 $数学公式$ 与C₁的异于极点的交点为A，与C₂的异于极点的交点为B，求|AB|．

解：（I）设P（x，y），则由条件知M（ y，x）．由于M点在C₁上，
所以 $\text{[math]}$ （θ为参数），
化成直角坐标方程为：x²+（y-2）²=4；
（Ⅱ）曲线C₁的极坐标方程为ρ=4cosθ，曲线C₂的极坐标方程为ρ=4sinθ．
射线θ= $\text{[math]}$ 与C₁的交点A的极径为ρ₁=4cos $\text{[math]}$ ，
射线θ= $\text{[math]}$ 与C₂的交点B的极径为ρ₂=4sin $\text{[math]}$ ．
所以|AB|=|ρ₂-ρ₁|=2 $\text{[math]}$ -2．
分析：（I）先设出曲线C₂上任一点P的坐标，然后根据曲线C₂与曲线C₁关于直线y=x对称得到点P满足的条件代入曲线C₁的方程即可求出曲线C₂的方程；
（II）根据（I）将求出曲线C₁的极坐标方程，分别求出射线θ= $\text{[math]}$ 与C₁的交点A的极径为ρ₁，以及射线θ= $\text{[math]}$ 与C₂的交点B的极径为ρ₂，最后根据|AB|=|ρ₂-ρ₁|求出所求．
点评：本题考查点的极坐标和直角坐标的互化，以及轨迹方程的求解和线段的度量，属于中档题．

练习册系列答案

西城学科专项测试系列答案

小考必做系列答案

小考实战系列答案

小考复习精要系列答案

小考总动员系列答案

小升初必备冲刺48天系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

萌齐小升初强化模拟训练系列答案

相关题目

[选修4-4：坐标系与参数方程]
在直角坐标系xoy中，直线l的参数方程为

（t为参数），若以直角坐标系xoy 的O点为极点，Ox为极轴，且长度单位相同，建立极坐标系，得曲线C的极坐标方程为ρ=2cos（θ-

）．直线l与曲线C交于A，B两点，求|AB|．

A．选修4-1：几何证明选讲
如图，△ABC的外接圆的切线AE与BC的延长线相交于点E，∠BAC的平分线与BC
交于点D．求证：ED²=EB•EC．
B．选修4-2：矩阵与变换
求矩阵M=

-1	4
2	6

的特征值和特征向量．
C．选修4-4：坐标系与参数方程
在以O为极点的极坐标系中，直线l与曲线C的极坐标方程分别是ρcos(θ+

和ρsin²θ=4cosθ，直线l与曲线C交于点．A，B，C，求线段AB的长．
D．选修4-5：不等式选讲
对于实数x，y，若|x-1|≤1，|y-2|≤1，求|x-y+1|的最大值．

（2013•辽宁）选修4-4：坐标系与参数方程
在直角坐标系xoy中以O为极点，x轴正半轴为极轴建立坐标系．圆C₁，直线C₂的极坐标方程分别为ρ=4sinθ，ρcos（θ-

．
（Ⅰ）求C₁与C₂交点的极坐标；
（Ⅱ）设P为C₁的圆心，Q为C₁与C₂交点连线的中点，已知直线PQ的参数方程为

（t∈R为参数），求a，b的值．

选修4-4：
坐标系与参数方程在平面直角坐标系x0y中，曲线C₁为x=acosφ，y=sinφ（1＜a＜6，φ为参数）．
在以0为原点，x轴正半轴为极轴的极坐标中，曲线C₂的方程为ρ=6cosθ，射线ι为θ=α，ι与C₁的交点为A，ι与C₂除极点外的一个交点为B．当α=0时，|AB|=4．
（1）求C₁，C₂的直角坐标方程；
（2）若过点P（1，0）且斜率为

的直线m与曲线C₁交于D、E两点，求|PD|与|PE|差的绝对值．

（2011•晋中三模）选修4-4：坐标系与参数方程选讲
在直角坐标系xoy中，曲线c₁的参数方程为：

（θ为参数），把曲线c₁上所有点的纵坐标压缩为原来的一半得到曲线c₂，以O为极点，x正半轴为极轴建立极坐标系，直线l的极坐标方程为

)=4．
（1）求曲线c₂的普通方程，并指明曲线类型；
（2）过（1，0）点与l垂直的直线l₁与曲线c₂相交与A、B两点，求弦AB的长．