题目内容
8.甲袋中装有5张奖券,其中3张10元的,2张20元的;乙袋中装有5张奖券都是10元的,所有奖券外形一样,现从甲袋中任取两张放入乙袋,搅拌均匀后再从乙袋中任取两张放入甲袋.(Ⅰ)求甲袋奖券中有且仅有一张20元的概率;
(Ⅱ)求甲袋中奖券总额X的分布列及数学期望.
分析 (Ⅰ)设从甲袋中取出的2张奖券中20元面值的有x张,从乙袋中取出的2张奖券中20元面值的有y张,该事件记为[x,y],利用互斥事件概率加法公式能求出甲袋奖券中有且仅有一张20元的概率.
(Ⅱ)X的可能取值为50,60,70,分别求出相应的概率,由此能求出X的分布列及数学期望EX.
解答 解:(Ⅰ)设从甲袋中取出的2张奖券中20元面值的有x张,从乙袋中取出的2张奖券中20元面值的有y张,该事件记为[x,y].
甲袋奖券中有且仅有一张20元的概率
P=P([2,1]+[1,0])=$\frac{{C}_{2}^{2}}{{C}_{5}^{2}}•\frac{{C}_{2}^{1}{C}_{5}^{1}}{{C}_{7}^{2}}+\frac{{C}_{2}^{1}{C}_{3}^{1}}{{C}_{7}^{2}}$=$\frac{10}{21}$.(5分)
(Ⅱ)X的可能取值为50,60,70.
P(X=50)=P([2,0])=$\frac{{C}_{2}^{2}}{{C}_{5}^{2}}•\frac{{C}_{5}^{2}}{{C}_{7}^{2}}$=$\frac{1}{21}$,
由(Ⅰ)得P(X=60)=$\frac{10}{21}$,
P(X=70)=P([2,2])+P([1,1])+P([0,0])
=$\frac{{C}_{2}^{2}}{{C}_{5}^{2}}•\frac{{C}_{2}^{2}}{{C}_{7}^{2}}$+$\frac{{C}_{2}^{1}{C}_{3}^{1}}{{C}_{5}^{2}}$•$\frac{{C}_{6}^{1}}{{C}_{7}^{2}}$+$\frac{{C}_{3}^{2}}{{C}_{5}^{2}}•\frac{{C}_{7}^{2}}{{C}_{7}^{2}}$=$\frac{10}{21}$.
∴X的分布列为
| X | 50 | 60 | 70 |
| P | $\frac{1}{21}$ | $\frac{10}{21}$ | $\frac{10}{21}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列、数学期望的求法,考查古典概型、排列组合、离散型随机变量的分布列及数学期望等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想,是中档题.

| A. | ($\frac{7π}{6}$,$\frac{4π}{3}$) | B. | [$\frac{7π}{6}$,$\frac{4π}{3}$] | C. | ($\frac{4π}{3}$,$\frac{3π}{2}$) | D. | [$\frac{4π}{3}$,$\frac{3π}{2}$] |
| A. | ?x∈R,x3≥x2 | B. | ?x∈R,x3<x2 | C. | ?x∈R,?y∈R,y2<x | D. | ?x∈R,?y∈R,y•x=y |
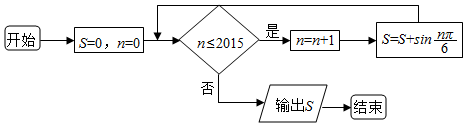
| A. | 0 | B. | $\frac{1}{2}$ | C. | $\frac{1}{2}$+$\frac{\sqrt{3}}{2}$ | D. | $\frac{3}{2}$+$\frac{\sqrt{3}}{2}$ |
| A. | {1,2} | B. | {0,1,2} | C. | {x|-2≤x≤2} | D. | {x|0≤x≤2} |