题目内容
曲线y=
x2-2在点（一1，-
）处的切线的倾斜角等于
- A.
- B.
- C.
- D.一
B
分析：先求出导函数，求出在切点处的导数值，即切线的斜率，利用切线的斜率时倾斜角的正切值，再根据倾斜角的范围求出倾斜角是常用的方法．
解答：y′=x2
令x=-1得到切线的斜率k═1
设倾斜角为α则tanα=k=1
∵0≤α≤π
∴
故选B．
点评：本题考查曲线在切点处的导数值是切线的斜率、考查直线的斜率与倾斜角的关系，要注意倾斜角的范围．属于基础题．
分析：先求出导函数，求出在切点处的导数值，即切线的斜率，利用切线的斜率时倾斜角的正切值，再根据倾斜角的范围求出倾斜角是常用的方法．
解答：y′=x2
令x=-1得到切线的斜率k═1
设倾斜角为α则tanα=k=1
∵0≤α≤π
∴
故选B．
点评：本题考查曲线在切点处的导数值是切线的斜率、考查直线的斜率与倾斜角的关系，要注意倾斜角的范围．属于基础题．
练习册系列答案
相关题目
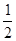x2-2在点（1，-1.5）和 点（-2，0）处的瞬时变化率的大小。
x2-2在点（一1，-
）处的切线的倾斜角等于（ ）
