题目内容
已知圆的方程为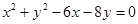 .设该圆过点
.设该圆过点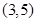 的最长弦和最短弦分别为AC和BD,则四边形ABCD的面积为( )
的最长弦和最短弦分别为AC和BD,则四边形ABCD的面积为( )
A.10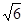 | B.20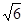 | C.30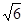 | D.40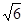 |
B
解析试题分析:圆的方程可整理为 .如图,设该圆圆心为
.如图,设该圆圆心为 ,
, 与
与 的交点为
的交点为 ,则
,则 ,
, ,故四边形
,故四边形 的面积为
的面积为 .
.
考点:圆的弦长及特征三角形.

练习册系列答案
相关题目
已知圆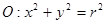 ,点
,点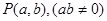 是圆
是圆 内的一点,过点
内的一点,过点 的圆
的圆 的最短弦在直线
的最短弦在直线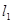 上,直线
上,直线 的方程为
的方程为 ,那么( )
,那么( )
A.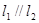 且 且 与圆 与圆 相交 相交 | B. 且 且 与圆 与圆 相切 相切 |
C.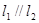 且 且 与圆 与圆 相离 相离 | D. 且 且 与圆 与圆 相离 相离 |
过点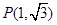 作圆
作圆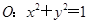 的两条切线,切点分别为
的两条切线,切点分别为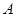 和
和 ,则弦长
,则弦长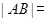 ( )
( )
A.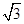 | B. | C. | D.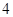 |
点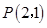 为圆
为圆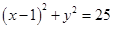 的弦
的弦 的中点,则直线
的中点,则直线 的方程为( )
的方程为( )
A. | B.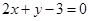 | C.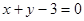 | D.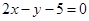 |
已知圆C1:(x-2)2+(y-3)2=1,圆C2:(x-3)2+(y-4)2=9,M,N分别是圆C1,C2上的动点,P为x轴上的动点,则|PM|+|PN|的最小值为( )
A.5 -4 -4 | B.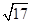 -1 -1 |
C.6-2 | D.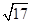 |
若原点在圆(x-m)2+(y+m)2=8的内部,则实数m的取值范围是( )
A.-2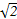 <m<2 <m<2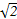 | B.0<m<2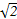 |
| C.-2<m<2 | D.0<m<2 |
已知点P(a,b)(ab≠0)是圆x2+y2=r2内的一点,直线m是以P为中点的弦所在的直线,直线l的方程为ax+by=r2,那么( )
| A.m∥l,且l与圆相交 | B.m⊥l,且l与圆相切 |
| C.m∥l,且l与圆相离 | D.m⊥l,且l与圆相离 |
已知圆(x-a)2+(y-b)2=r2的圆心为抛物线y2=4x的焦点,且与直线3x+4y+2=0相切,则该圆的方程为( ).
A.(x-1)2+y2= | B.x2+(y-1)2= |
| C.(x-1)2+y2=1 | D.x2+(y-1)2=1 |