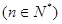题目内容
设函数
(1)若关于x的不等式 在
在 有实数解,求实数m的取值范围;
有实数解,求实数m的取值范围;
(2)设 ,若关于x的方程
,若关于x的方程 至少有一个解,求p的最小值.
至少有一个解,求p的最小值.
(3)证明不等式:

【答案】
(1) (2)p的最小值为0
(2)p的最小值为0
【解析】
试题分析:
(1)存在性问题,只需要 即可,再利用导数法求解f(x)的最大值(即求导,求单调性,求极值9与端点值比较得出最值).
即可,再利用导数法求解f(x)的最大值(即求导,求单调性,求极值9与端点值比较得出最值).
(2)p的最小值为函数g(x)的最小值,利用导数求函数的最小值即可(即求导,求单调性,求极值9与端点值比较得出最值).
(3)利用第二问结果可以得到与不等式有关的恒等式 .令
.令 .把n=1,2,3,,得n个不等式左右相加,左边利用对数除法公式展开即可用裂项求和法得到不等式的左边,即证得原式
.把n=1,2,3,,得n个不等式左右相加,左边利用对数除法公式展开即可用裂项求和法得到不等式的左边,即证得原式
试题解析:
(1)依题意得
 ,而函数
,而函数 的定义域为
的定义域为
∴ 在
在 上为减函数,在
上为减函数,在 上为增函数,则
上为增函数,则 在
在 上为增函数
上为增函数
, 即实数m的取值范围为
即实数m的取值范围为 4分
4分
(2)
 则
则
显然,函数 在
在 上为减函数,在
上为减函数,在 上为增函数,则函数
上为增函数,则函数 的最小值为
的最小值为
所以,要使方程 至少有一个解,则
至少有一个解,则 ,即p的最小值为0 8分
,即p的最小值为0 8分
(3)由(2)可知:  在
在 上恒成立
上恒成立
所以  ,当且仅当x=0时等号成立
,当且仅当x=0时等号成立
令 ,则
,则 代入上面不等式得:
代入上面不等式得:
即 , 即
, 即 
所以, ,
, ,
, ,,
,,
将以上n个等式相加即可得到: 12分
12分
考点:导数 不等式 函数最值

练习册系列答案
相关题目

 在
在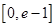 有实数解,求实数m的取值范围;
有实数解,求实数m的取值范围; ,若关于x的方程
,若关于x的方程 至少有一个解,求
至少有一个解,求 的最小值.
的最小值.

 在
在 有实数解,求实数m的取值范围;
有实数解,求实数m的取值范围; ,若关于x的方程
,若关于x的方程 至少有一个解,求p 的最小值.
至少有一个解,求p 的最小值.

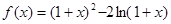
 在
在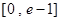 有实数解,求实数m的取值范围;
有实数解,求实数m的取值范围;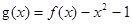 ,若关于x的方程
,若关于x的方程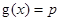 至少有一个解,求p 的最小值.
至少有一个解,求p 的最小值.
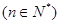
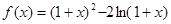
 在
在 有实数解,求实数m的取值范围;
有实数解,求实数m的取值范围; ,若关于x的方程
,若关于x的方程 至少有一个解,求p 的最小值.
至少有一个解,求p 的最小值.

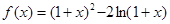
 在
在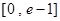 有实数解,求实数m的取值范围;
有实数解,求实数m的取值范围; ,若关于x的方程
,若关于x的方程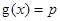 至少有一个解,求p 的最小值.
至少有一个解,求p 的最小值.