Question

已知函数f(x)=4x3-3x2cosθ+

3

16

cosθ，其中x∈R，θ为参数，且0≤θ≤2π．
（Ⅰ）当cosθ=0时，判断函数f（x）是否有极值；
（Ⅱ）要使函数f（x）的极小值大于零，求参数θ的取值范围；
（Ⅲ）若对（2）中所求的取值范围内的任意参数θ，函数f（x）在区间（2a-1，a）内都是增函数，求实数a的取值范围．

Answer 1

分析：（I）先求函数的导数，f′（x）＞0在（-∞，+∞）上恒成立，得到函数的单调性，从而可判定是否有极值．
（II）先求出极值点，f′（x）=0的点附近的导数的符号的变化情况，来确定极值，求出极小值，使函数f（x）的极小值小于零建立不等关系，求出参数θ的取值范围即可．
（III）由②知，函数f（x）在区间（-∞，0）与 （

cosθ

2

，+∞）内都是增函数，只需（2a-1，a）是区间（-∞，0）与 （

cosθ

2

，+∞）的子集即可．

解答：解：（Ⅰ）（1）当cosθ=0时，f（x）=4x³，则f（x）在（-∞，+∞）内是增函数，故无极值．
（II）f'（x）=12x²-6xcosθ，令f′（x）=0，得x₁=0，x2=

cosθ

2

．由（1）知，只需分下面两种情况讨论．
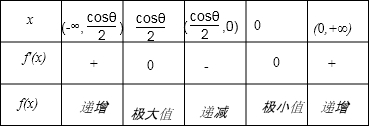
（1）当cosθ＞0时，随x的变化f′（x）的符号及f（x）的变化情况如下表：

∴f（x）在x=

cosθ

2

处取得极小值，且f（

cosθ

2

）=-

cos3θ

4

+

3cosθ

16

＞0
∴0＜cosθ＜

3

2

∴

π

6

＜θ＜

π

2

或

3π

2

＜θ＜

11π

6

（2）cos θ＜0时，随x的变化f′（x）的符号及f（x）的变化情况如下表：

∵f（x）在x=0处取得极小值f（0），且f（0）=

3cosθ

16

若f（0）＞0则cosθ＞0与已知cosθ＜0矛盾
∴当cosθ＜0时，f（x）的极大值不会大于0
综上可得，要使得函数f（x）在R上的极小值大于0，θ∈(

π

6

，

π

2

)∪(

3π

2

，

11π

6

)
（III）由（II）知，函数f（x）在区间（-∞，0）与 （

1

2

cosθ，+∞）内都是增函数．
由题设，函数f（x）在（2a-1，a）内是增函数，
则a须满足不等式组 

2a-1＜a a≤0

    或 

2a-1＜a 2a-1≥ cosθ 2

 由（II），θ∈(

π

6

，

π

2

)∪(

3π

2

，

11π

6

)时，0＜cosθ＜

3

2

要使不等式 2a-1≥

1

2

cosθ关于参数θ恒成立，必有 2a-1≥

3

4

∴a≥

4+ 3

8

综上可得，a≤0或

4+ 3

8

≤a＜1

点评：本小题主要考查运用导数研究函数的单调性及极值、解不等式等基础知识，考查综合分析和解决问题的能力．