题目内容
已知 ,P1(x1,y1)、P2(x2,y2)是函数y=f(x)图象上两点,且线段P1P2中点P的横坐标是
,P1(x1,y1)、P2(x2,y2)是函数y=f(x)图象上两点,且线段P1P2中点P的横坐标是 .
.(1)求证点P的纵坐标是定值;
(2)若数列{an}的通项公式是
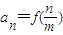 (m∈N*),n=1,2…m),求数列{an}的前m项和Sm;
(m∈N*),n=1,2…m),求数列{an}的前m项和Sm; (3)在(2)的条件下,若m∈N*时,不等式
 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
【答案】分析:(1)由 知,x1+x2=1,故y1+y2=
知,x1+x2=1,故y1+y2=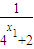 +
+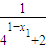 ,由此能够证明点P的纵坐标是定值.
,由此能够证明点P的纵坐标是定值.
(2)已知Sm=a1+a2+…+am=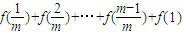 ,利用倒序相加法能够求出数列{an}的前m项和Sm.
,利用倒序相加法能够求出数列{an}的前m项和Sm.
(3)由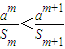 ,得12am(
,得12am( -
- )<0对m∈N+恒成立.由此利用分类讨论思想能够求出实数a的取值范围.
)<0对m∈N+恒成立.由此利用分类讨论思想能够求出实数a的取值范围.
解答:解:(1)由 知,x1+x2=1,则
知,x1+x2=1,则
y1+y2=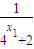 +
+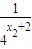
=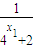 +
+
=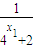 +
+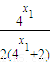
= ,
,
故点P的纵坐标是 ,为定值.
,为定值.
(2)已知Sm=a1+a2+…+am
=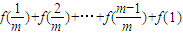 ,
,
又Sm=am-1+am-2+…+a1+am
=f(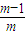 )+f(
)+f(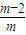 )+…+f(
)+…+f(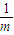 )+f(1)
)+f(1)
二式相加,得
 +
+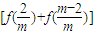 +…+
+…+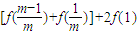 ,
,
因为 ,…m-1),故
,…m-1),故 ,
,
又f(1)=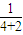 =
= ,从而
,从而 .(12分)
.(12分)
(3)由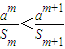 ,
,
得12am(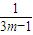 -
-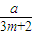 )<0…①对m∈N+恒成立.
)<0…①对m∈N+恒成立.
显然,a≠0,
(ⅰ)当a<0时,由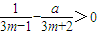 ,得am<0.
,得am<0.
而当m为偶数时am<0不成立,所以a<0不合题意;
(ⅱ)当a>0时,因为am>0,
则由式①得,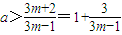 .
.
又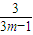 随m的增大而减小,
随m的增大而减小,
所以,当m=1时,1+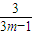 有最大值
有最大值 ,故a
,故a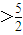 .(18分)
.(18分)
点评:本题考查点的纵坐标是定值的证明,考查数列的前n项和的求法,考查实数的取值范围的求法,解题时要认真审题,注意倒序相加法、分类讨论思想的灵活运用.
 知,x1+x2=1,故y1+y2=
知,x1+x2=1,故y1+y2=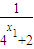 +
+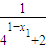 ,由此能够证明点P的纵坐标是定值.
,由此能够证明点P的纵坐标是定值.(2)已知Sm=a1+a2+…+am=
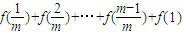 ,利用倒序相加法能够求出数列{an}的前m项和Sm.
,利用倒序相加法能够求出数列{an}的前m项和Sm.(3)由
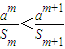 ,得12am(
,得12am( -
- )<0对m∈N+恒成立.由此利用分类讨论思想能够求出实数a的取值范围.
)<0对m∈N+恒成立.由此利用分类讨论思想能够求出实数a的取值范围.解答:解:(1)由
 知,x1+x2=1,则
知,x1+x2=1,则y1+y2=
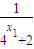 +
+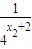
=
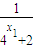 +
+
=
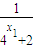 +
+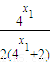
=
 ,
,故点P的纵坐标是
 ,为定值.
,为定值.(2)已知Sm=a1+a2+…+am
=
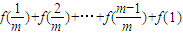 ,
,又Sm=am-1+am-2+…+a1+am
=f(
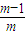 )+f(
)+f(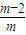 )+…+f(
)+…+f(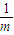 )+f(1)
)+f(1)二式相加,得
 +
+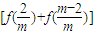 +…+
+…+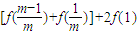 ,
,因为
 ,…m-1),故
,…m-1),故 ,
,又f(1)=
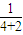 =
= ,从而
,从而 .(12分)
.(12分)(3)由
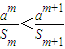 ,
,得12am(
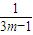 -
-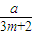 )<0…①对m∈N+恒成立.
)<0…①对m∈N+恒成立.显然,a≠0,
(ⅰ)当a<0时,由
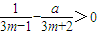 ,得am<0.
,得am<0.而当m为偶数时am<0不成立,所以a<0不合题意;
(ⅱ)当a>0时,因为am>0,
则由式①得,
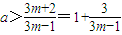 .
.又
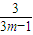 随m的增大而减小,
随m的增大而减小,所以,当m=1时,1+
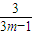 有最大值
有最大值 ,故a
,故a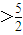 .(18分)
.(18分)点评:本题考查点的纵坐标是定值的证明,考查数列的前n项和的求法,考查实数的取值范围的求法,解题时要认真审题,注意倒序相加法、分类讨论思想的灵活运用.

练习册系列答案
相关题目