题目内容

已知点P1（x1，y1）是直线l：f（x，y）=0上的一点，P2（x2，y2）是直线l外的一点，则f（x，y）-f（x1，y1）-f（x2，y2）=0方程表示的直线l的位置关系是
平行
平行
分析：P1满足直线方程，∴f（x1，y1）=0，P2不满足直线方程，∴f（x2，y2）≠0．化简f（x，y）-f（x1，y1）-f（x2，y2）=0，分析此时的直线和直线l：f（x，y）=0平行．
解答：解：∵P1在l上，∴f（x1，y1）=0．
∴P2不在直线l上，∴f（x2，y2）≠0．
∴f（x，y）-f（x1，y1）-f（x2，y2）=0?f（x，y）-f（x2，y2）=0．
∴方程表示过点P2且平行于l的直线．
故答案：平行
点评：用好条件，逐步求解，往往是解数学问题的一般规律和方法．
练习册系列答案
相关题目
已知点P1（x1，y1）、P2（x2，y2）分别在直线l上和在l外，若直线l的方程为f（x，y）=0，则方程f（x，y）-f（x1，y1）-f（x2，y2）=0表示（　　）
（2013•杨浦区一模）设数列{xn}满足xn≠1且（n∈N*），前n项和为Sn．已知点p1（x1，S1），P2（x2，s2），…Pn（xn，sn）都在直线y=kx+b上（其中常数b，k且k≠1，b≠0），又yn=log
12
 xn．
（1）求证：数列{xn]是等比数列；
（2）若yn=18-3n，求实数k，b的值；
（3）如果存在t、s∈N*，s≠t使得点（t，yt）和点（s，yt）都在直线y=2x+1上．问是否存在正整数M，当n＞M时，xn＞1恒成立？若存在，求出M的最小值，若不存在，请说明理由．
设数列{xn}满足xn≠1且（n∈N*），前n项和为Sn．已知点p1（x1，S1），P2（x2，s2），…Pn（xn，sn）都在直线y=kx+b上（其中常数b，k且k≠1，b≠0），又yn=log．
（1）求证：数列{xn]是等比数列；
（2）若yn=18-3n，求实数k，b的值；
（3）如果存在t、s∈N*，s≠t使得点（t，yt）和点（s，yt）都在直线y=2x+1上．问是否存在正整数M，当n＞M时，xn＞1恒成立？若存在，求出M的最小值，若不存在，请说明理由．
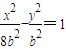已知点P1（x，y）为双曲线（b为正常数）上任一点，F2为双曲线的右焦点，过P1作右准线的垂线，垂足为A，连接F2A并延长交y轴于P2．
（1）求线段P1P2的中点P的轨迹E的方程；
（2）设轨迹E与x轴交于B、D两点，在E上任取一点Q（x1，y1）（y1≠0），直线QB，QD分别交y轴于M，N两点．求证：以MN为直径的圆过两定点．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网