题目内容
如图,已知三棱柱ABC—A1B1C1的底面是边长为2的正三角形,侧棱A1A与AB、AC均成45°角,且A1E⊥B1B于E,A1F⊥CC1于F.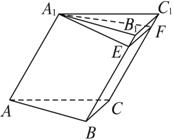
(1)求证:平面A1EF⊥平面B1BCC1;
(2)求直线AA1到平面B1BCC1的距离;
(3)当AA1多长时,点A1到平面ABC与平面B1BCC1的距离相等?
解:(1)证明:CC1∥BB1,又BB1⊥A1E,∴CC1⊥A1E.而CC1⊥A1F,
∴CC1⊥平面A1EF,∴平面A1EF⊥平面B1BCC1.
(2)作A1H⊥EF于H,则A1H⊥面B1BCC1,∴A1H为A1到面B1BCC1的距离.在△A1EF中,A1E=A1F=2,EF=2,∴△A1EF为等腰直角三角形且EF为斜边,∴A1H为斜边上中线,可得A1H=![]() EF=1.
EF=1.
(3)作A1G⊥面ABC于G,连结AG,则A1G就是A1到面ABC的距离,且AG是∠BAC的角平分线,A1G=1.
∵cos∠A1AG=![]() .∴sin∠A1AG=
.∴sin∠A1AG=![]() .∴A1A=
.∴A1A=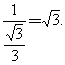

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
 如图,已知三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AC=BC=2,AA1=4,
如图,已知三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AC=BC=2,AA1=4, 如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,且AB⊥AC,M是CC1的中点,N是BC的中点,点P在直线A1B1上,且满足
如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,且AB⊥AC,M是CC1的中点,N是BC的中点,点P在直线A1B1上,且满足 如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M,N分别是CC1,BC的中点,点P在直线A1B1上,且
如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M,N分别是CC1,BC的中点,点P在直线A1B1上,且 如图,已知三棱柱ABC-A1B1C1的所有棱长均为2,且A1A⊥底面ABC,D为AB的中点,G为△ABC1的重心,则|
如图,已知三棱柱ABC-A1B1C1的所有棱长均为2,且A1A⊥底面ABC,D为AB的中点,G为△ABC1的重心,则| 如图,已知三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=BC,∠ABC=90°,D为AC中点.
如图,已知三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=BC,∠ABC=90°,D为AC中点.