题目内容
已知函数 .
.
(I)判断函数f(x)的奇偶性;
(II)判断函数f(x)在(1,+∞)上的单调性;
(III)求函数f(x)在[2,4]上的最大和最小值.
解:(I)函数的定义域为{x|x≠0},
对任意不等于0的实数f(-x)=
所以函数为奇函数
(II)f′(x)=1-
∵x>1
∴
∴
∴f′(x)>0
∴函数f(x)在(1,+∞)上是增函数
(III)
由(II)知函数f(x)在[2,4]上是增函数
∴当x=2时,函数函数f(x)取得最小值为f(2)=
分析:(I)先求函数定义域,看是否关于原点对称,再探讨f(x)与f(-x)间的关系.若相等,则为偶函数;若相反,则为奇函数.
(II)用导数法,先求导,再分析在(1,+∞)上导数的正负.若导数大于零时则为增函数;若导数小于零时则为减函数.
(III)由[2,4]是(1,+∞)的真子集,则用(II)的单调性来求最值.若为增函数,则2,4分别对应最小值和最大值;若为减函数,则2,4分别对应最大值和最小值.
点评:本题主要考查函数的奇偶性和单调性,要注意判断和证明是不同的,判断可用一些常用的结论,但证明奇偶性时只有定义法,证明单调性时要用定义法和导数法.同时还考查了求函数最值问题,在研究此类问题时,要注意先研究单调性.
对任意不等于0的实数f(-x)=

所以函数为奇函数
(II)f′(x)=1-

∵x>1
∴

∴

∴f′(x)>0
∴函数f(x)在(1,+∞)上是增函数
(III)
由(II)知函数f(x)在[2,4]上是增函数
∴当x=2时,函数函数f(x)取得最小值为f(2)=

分析:(I)先求函数定义域,看是否关于原点对称,再探讨f(x)与f(-x)间的关系.若相等,则为偶函数;若相反,则为奇函数.
(II)用导数法,先求导,再分析在(1,+∞)上导数的正负.若导数大于零时则为增函数;若导数小于零时则为减函数.
(III)由[2,4]是(1,+∞)的真子集,则用(II)的单调性来求最值.若为增函数,则2,4分别对应最小值和最大值;若为减函数,则2,4分别对应最大值和最小值.
点评:本题主要考查函数的奇偶性和单调性,要注意判断和证明是不同的,判断可用一些常用的结论,但证明奇偶性时只有定义法,证明单调性时要用定义法和导数法.同时还考查了求函数最值问题,在研究此类问题时,要注意先研究单调性.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
 .
. 的图象总在直线y=a的上方,求实数a的取值范围;
的图象总在直线y=a的上方,求实数a的取值范围; 的图象有公共点,且在公共点处的切线相同,求实数m的值.
的图象有公共点,且在公共点处的切线相同,求实数m的值. .
. 的图象总在直线y=a的上方,求实数a的取值范围;
的图象总在直线y=a的上方,求实数a的取值范围; 的图象有公共点,且在公共点处的切线相同,求实数m的值.
的图象有公共点,且在公共点处的切线相同,求实数m的值. .
. 的奇偶性;
的奇偶性; 上的最小值为
上的最小值为 ,求
,求 ,证明:方程
,证明:方程 有两个不同的正数解.
有两个不同的正数解.  .
. 在
在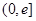 上的单调性(
上的单调性(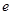 为自然对数的底);
为自然对数的底); 为
为 的导函数,若函数
的导函数,若函数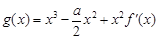 在区间
在区间 上存在极值,求实数
上存在极值,求实数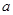 的取值范围。
的取值范围。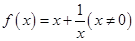 。
。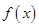 的奇偶性;
的奇偶性;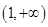 上的单调性;
上的单调性;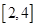 上的最大和最小值。
上的最大和最小值。