Question

如图，四棱锥S—ABCD的底面是边长为1的正方形，SD垂直于底面ABCD ，SB=.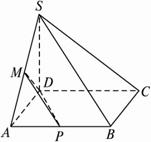

（1）求证：BC⊥SC；

（2）求面SAD与面SBC所成二面角的大小；

（3）设棱SA的中点为M，求异面直线DM与SB所成角的大小.

Answer 1

解析：第（1）题要证BC⊥SC，只需证明BC⊥CD即可，由已知条件和三垂线定理可以证明BC⊥SC，当然也可以直接利用线面垂直来证BC⊥SC.对于第（2）题的解题策略是先找出两面的交线.然后直觉预见∠CSD是二面角的平面角，最后再计算；另外一种思路就是利用△SBC在面SAD上的射影是△SAD，再用cosθ=求出θ的值就是二面角的大小.对于第（3）题是求异面直线所成的角.平移SB且过M点既可转化为平面内的角求解,还可以直接利用三垂线定理证明SB⊥MD，于是也就求出MD与SB所成的角.?

（1）证法一：∵底面ABCD是正方形，?

∴BC⊥DC.?

?  ∵SD⊥底面ABCD，?

∴DC是SC在平面ABCD上的射影，由三垂线定理得BC⊥SC.?

证法二：∵底面ABCD是正方形，?

∴BC⊥DC.?

∵SD⊥底面ABCD，?

∴SD⊥BC.?

又DC∩SD=D，∴BC⊥平面SDC.?

∴BC⊥SC.?

（2）解法一：∵S是面SAD与面SBC的公共点，?

∴设面SAD∩面SBC=l.?

∵ABCD是正方形，∴AD∥BC.?

∴BC∥面SAD.?

又BC面SBC，∴BC∥l.?

∴BC∥l∥AD.?

又∵SD⊥面ABCD，?

∴SD⊥AD,即SD⊥l.?

又由（1）知BC⊥SC，?

∴SC⊥l.?

∴∠CSD是二面角C-l-A的平面角.?

在Rt△SCB中，由勾股定理得.?

在Rt△SCD中，sin∠CSD=CDSC=,?

∴∠CSD=45°,即面ASD与面BSC所成的二面角为45°.?

解法二：∵SD⊥面ABCD，?

∴SD⊥CD.?

又∵ABCD是正方形，∴CD⊥AD.?

而AD∩SD=D，∴CD⊥面SAD.?

又由ABCD是正方形可知，CD∥AB，?

∴AB⊥面SAD.?

∴△SBC在侧面SAD上的射影是△SAD.?

设面ASD与面BSC所成的二面角大小为θ,?

∴cosθ=.又由（1）知，在Rt△SBC中，SB=，BC=1，∴SC=.

在Rt△SCD中，SD=1，?

∴,.??

∴cosθ=.?

∴θ=45°,即面ASD与面BSC所成的二面角为45°.?

（3）解法一：（平移法）取AB中点P，连结MP、DP.在△ABS中，由中位线定理得MP∥SB，∴∠DMP是异面直线DM与SB所成的角.?

∵，又， .

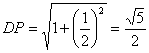∴在△DMP中，有DP²=MP²+DM².?

∴∠DMP=90°.?

∴异面直线DM与SB所成的角为90°.?

解法二：（三垂线定理法）∵SD=AD=1，∠SDA=90°,?

∴△SDA是等腰直角三角形.?

又∵M是斜边SA的中点，?

?∴DM⊥SA.?

∵BA⊥AD，BA⊥SD，AD∩SD=D，?

∴BA⊥面ASD.?

∴SA是SB在面SAD上的射影.?

由三垂线定理知DM⊥SB.?

∴异面直线DM与SB所成的角为90°.