题目内容
.(本小题满分12分)对于函数 ,若
,若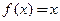 ,则称
,则称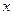 为
为 的“不动点”,若
的“不动点”,若 ,则称
,则称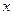 为
为 的“稳定点”.函数的“不动点”和“稳定点”的集合分别记为
的“稳定点”.函数的“不动点”和“稳定点”的集合分别记为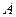 和
和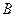 ,即
,即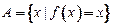 ,
, .
.
(1)求证: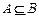 ;
;
(2)若 ,且
,且 ,求实数
,求实数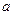 的取值范围;
的取值范围;
(3)若 是
是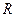 上的单调递增函数,
上的单调递增函数,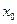 是函数的稳定点,问
是函数的稳定点,问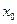 是函数的不动点吗?若是,请证明你的结论;若不是,请说明的理由.
是函数的不动点吗?若是,请证明你的结论;若不是,请说明的理由.
 ,若
,若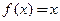 ,则称
,则称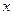 为
为 的“不动点”,若
的“不动点”,若 ,则称
,则称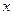 为
为 的“稳定点”.函数的“不动点”和“稳定点”的集合分别记为
的“稳定点”.函数的“不动点”和“稳定点”的集合分别记为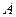 和
和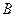 ,即
,即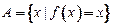 ,
, .
.(1)求证:
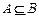 ;
;(2)若
 ,且
,且 ,求实数
,求实数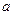 的取值范围;
的取值范围; (3)若
 是
是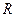 上的单调递增函数,
上的单调递增函数,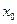 是函数的稳定点,问
是函数的稳定点,问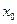 是函数的不动点吗?若是,请证明你的结论;若不是,请说明的理由.
是函数的不动点吗?若是,请证明你的结论;若不是,请说明的理由.解:(1)若 ,则
,则 显然成立;若
显然成立;若 ,设
,设 ,
,
则 ,
, ,故
,故 . …………3分
. …………3分
(2) 有实根,
有实根, .又
.又 ,所以
,所以 ,
,
即 的左边有因式
的左边有因式 ,
,
从而有 . …………5分
. …………5分
 ,
, 要么没有实根,要么实根是方程
要么没有实根,要么实根是方程 的根.若
的根.若 没有实根,
没有实根,
则 ;若
;若 有实根且实根是方程
有实根且实根是方程 的根,
的根,
则由方程 ,得
,得 ,
,
代入 ,有
,有 .由此解得
.由此解得 ,再代入得
,再代入得 ,由此
,由此 ,
,
故a的取值范围是 . …………8分
. …………8分
(3)由题意: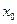 是函数的稳定点则
是函数的稳定点则 ,设
,设 ,
,
 是
是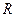 上的单调增函数,则
上的单调增函数,则 ,
,
所以 ,矛盾.
,矛盾.
若 ,
, 是
是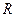 上的单调增函数,则
上的单调增函数,则 ,
,
所以 ,矛盾,故
,矛盾,故 ,
,
所以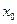 是函数的不动点. …………12分
是函数的不动点. …………12分
 ,则
,则 显然成立;若
显然成立;若 ,设
,设 ,
,则
 ,
, ,故
,故 . …………3分
. …………3分(2)
 有实根,
有实根, .又
.又 ,所以
,所以 ,
,即
 的左边有因式
的左边有因式 ,
,从而有
 . …………5分
. …………5分 ,
, 要么没有实根,要么实根是方程
要么没有实根,要么实根是方程 的根.若
的根.若 没有实根,
没有实根,则
 ;若
;若 有实根且实根是方程
有实根且实根是方程 的根,
的根,则由方程
 ,得
,得 ,
,代入
 ,有
,有 .由此解得
.由此解得 ,再代入得
,再代入得 ,由此
,由此 ,
,故a的取值范围是
 . …………8分
. …………8分(3)由题意:
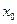 是函数的稳定点则
是函数的稳定点则 ,设
,设 ,
, 是
是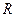 上的单调增函数,则
上的单调增函数,则 ,
,所以
 ,矛盾.
,矛盾.若
 ,
, 是
是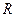 上的单调增函数,则
上的单调增函数,则 ,
,所以
 ,矛盾,故
,矛盾,故 ,
,所以
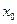 是函数的不动点. …………12分
是函数的不动点. …………12分略

练习册系列答案
相关题目
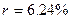 ,2000年该奖发放后基金总额约为21000万元。用
,2000年该奖发放后基金总额约为21000万元。用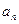
 表示为第
表示为第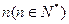 年该奖发放后的基金总额(2000年为第一年)。
年该奖发放后的基金总额(2000年为第一年)。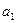 表示
表示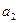 与
与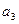 ,并根据所求结果归纳出
,并根据所求结果归纳出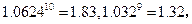
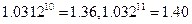 )
)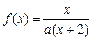 ,方程
,方程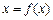 有唯一解,其中实数
有唯一解,其中实数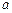 为常数,
为常数,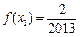 ,
,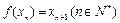
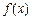 的表达式;
的表达式;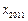 的值;
的值;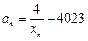 且
且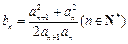 ,求证:
,求证: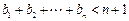
 的图象同时经过第一、三、四象限的必要但不充分条件是( )
的图象同时经过第一、三、四象限的必要但不充分条件是( ) 且
且 B
B  C
C  且
且 D
D  且
且 满足
满足 ,并且当
,并且当 时
时 ,
, ,求当
,求当 时,
时,
 .
. 在闭区间
在闭区间 上的最大值称为
上的最大值称为 在闭区间
在闭区间 ,则
,则 = 。
= 。 有零点的区间是( )
有零点的区间是( )



 的单调递减区间是 .
的单调递减区间是 . 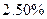 保持不变,到2015年9月1日将所有的存款和利息全部取出,他可取回的钱数约为
保持不变,到2015年9月1日将所有的存款和利息全部取出,他可取回的钱数约为  【 】
【 】