Question

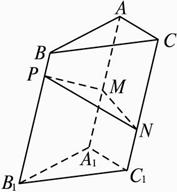
如图2-2-1,两个完全相等的正方形ABCD和ABEF不在同一平面内,点M、N分别在它们的对角线AC、BF上,且CM=BN.求证:MN∥平面BCE.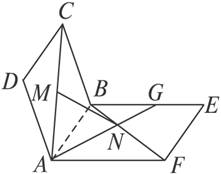

图2-2-1

Answer 1

思路分析:证明线面平行,常常需利用线线平行,即根据判定定理来说明,其中的关键是在平面内构造与已知直线平行的直线.

证明:连结AN并延长交BE于G点.

∵AF∥BE,∴.

∵正方形ABCD与正方形ABEF全等,∴AC=BF.

∵CM=BN,∴MA=NF.

∵,∴MN∥CG.

∵CG平面BCE,MN平面BCE,

∴MN∥平面BCE.

  绿色通道:由于两条平行线确定一个平面,所以在平面α内找与平面外的直线l的平行线时,通常过l作一个平面β与α相交,再设法证l与α,β的交线平行.