题目内容
已知关x的方25x2-35x+m=0的两根为sin和cos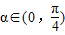
(1)m的值 (2)求sinα-cosα的值 (3)求
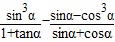 的值.
的值.
【答案】分析:(1)利用查韦达定理、同角三角函数的基本关系,待定系数法求得m=12.
(2)根据角α的范围可得sinα-cosα=- =
= ,把sinα•cosα=
,把sinα•cosα= =
=
代入,运算求得结果.
(3)由(1)求得sinα= 、cosα=
、cosα= 、tanα=
、tanα= ,代入要求的式子化简可得它的值.
,代入要求的式子化简可得它的值.
解答:解:(1)由题意可得sinα+cosα= ,sinα•cosα=
,sinα•cosα= ,
, .
.
化简可得 1+2sinα•cosα=1+ =
= ,∴m=12.
,∴m=12.
(2)∵ ,∴sinα<cosα,
,∴sinα<cosα,
∴sinα-cosα=- =-
=- =-
=- .
.
(3)由(1)得sinα+cosα= ,sinα•cosα=
,sinα•cosα= ,
, .
.
∴sinα= ,cosα=
,cosα= ,tanα=
,tanα= .
.
∴ =
= -
- =
= -
- =
= .
.
点评:本题考查韦达定理、同角三角函数的基本关系的应用,求出sinα= 、cosα=
、cosα= 、tanα=
、tanα= ,是解题的关键.
,是解题的关键.
(2)根据角α的范围可得sinα-cosα=-
 =
= ,把sinα•cosα=
,把sinα•cosα= =
=
代入,运算求得结果.
(3)由(1)求得sinα=
 、cosα=
、cosα= 、tanα=
、tanα= ,代入要求的式子化简可得它的值.
,代入要求的式子化简可得它的值.解答:解:(1)由题意可得sinα+cosα=
 ,sinα•cosα=
,sinα•cosα= ,
, .
.化简可得 1+2sinα•cosα=1+
 =
= ,∴m=12.
,∴m=12.(2)∵
 ,∴sinα<cosα,
,∴sinα<cosα,∴sinα-cosα=-
 =-
=- =-
=- .
.(3)由(1)得sinα+cosα=
 ,sinα•cosα=
,sinα•cosα= ,
, .
.∴sinα=
 ,cosα=
,cosα= ,tanα=
,tanα= .
.∴
 =
= -
- =
= -
- =
= .
.点评:本题考查韦达定理、同角三角函数的基本关系的应用,求出sinα=
 、cosα=
、cosα= 、tanα=
、tanα= ,是解题的关键.
,是解题的关键. 
练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目