题目内容
在正三棱柱ABC—A1B1C1中,底面边长为a,D为BC为中点,M在BB1上,且BM=(1)求证:CM⊥C1D;
(2)求AA1的长.
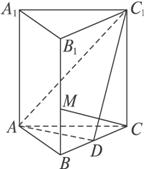
(1)证明:在正三棱柱ABC—A1B1C1中,D为BC中点,则AD⊥面BCC1B1,从而AD⊥MC.
又∵CM⊥AC1,则MC和平面ADC1内两相交直线AD,AC1均垂直,
∴MC⊥面ADC1,于是MC⊥DC1.
(2)解:在矩形BB1C1C中,由CM⊥DC1,
知△DCC1∽△BMC,设BB1=h,则BM=![]() h,∴
h,∴![]() h:a=
h:a=![]() ∶h,
∶h,
求得h=![]() a,从而所求AA1=
a,从而所求AA1=![]() a.
a.

练习册系列答案
相关题目
 如图,在正三棱柱ABC-A1B1C1中,AA1=AB,D是AC的中点.
如图,在正三棱柱ABC-A1B1C1中,AA1=AB,D是AC的中点.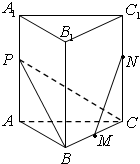 如图,在正三棱柱ABC-A1B1C1中,所有棱的长度都是1,M是BC边的中点,P是AA1边上的点,且
如图,在正三棱柱ABC-A1B1C1中,所有棱的长度都是1,M是BC边的中点,P是AA1边上的点,且 如图,在正三棱柱ABC-A'B'C'中,AB=2,若二面角C'-AB-C的大小为60°,则点C到平面ABC'的距离为
如图,在正三棱柱ABC-A'B'C'中,AB=2,若二面角C'-AB-C的大小为60°,则点C到平面ABC'的距离为