Question

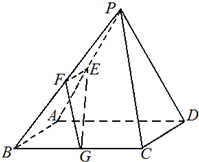（2012•安徽模拟）已知在四棱锥P-ABCD中，底面ABCD是边长为4的正方形，△PAD是正三角形，平面PAD⊥平面ABCD，E、F、G分别是PA、PB、BC的中点．
（I）求证：EF⊥平面PAD；
（II）求平面EFG与平面ABCD所成锐二面角的大小．

Answer 1

分析：（I）先根据平面PAD⊥平面ABCD，AB⊥AD得到AB⊥平面PAD；再结合EF∥AB，即可得到EF⊥平面PAD；
（II）过P作AD的垂线，垂足为O，根据平面PAD⊥平面ABCD，得PO⊥平面ABCD；再取AO中点M，连OG得到OG即为面EFG与面ABCD的交线；最后根据EM⊥平面ABCD．且OG⊥AO，得到的OG⊥EO求出∠EOM 即可．

解答：解：（I）证明：∵平面PAD⊥平面ABCD，AB⊥AD，
∴AB⊥平面PAD，（4分）
∵E、F为PA、PB的中点，
∴EF∥AB，
∴EF⊥平面PAD；                        （6分）
（II）解：过P作AD的垂线，垂足为O，
∵平面PAD⊥平面ABCD，则PO⊥平面ABCD．
取AO中点M，连OG，EO，EM，
∵EF∥AB∥OG，
∴OG即为面EFG与面ABCD的交线（8分）
又EM∥OP，则EM⊥平面ABCD．且OG⊥AO，
故OG⊥EO
∴∠EOM 即为所求       （11分）
在RT△EOM中，EM=

3

OM=1
∴tan∠EOM=

3

，故∠EOM=60°
∴平面EFG与平面ABCD所成锐二面角的大小是60°．（14分）

点评：本题主要考察直线与平面垂直的判定以及二面角的求法．解决第二问的难点在于找到两半平面的交线，进而求出二面角的平面角．