Question

【题目】正四面体ABCD中，M是棱AD的中点，O是点A在底面BCD内的射影，则异面直线BM与AO所成角的余弦值为（ ）
A.
B.
C.
D.

Answer 1

【答案】B
【解析】解：取BC中点E，DC中点F，连结DE、BF，则由题意得DE∩BF=O， 取OD中点N，连结MN，则MN∥AO，
∴∠BMN是异面直线BM与AO所成角（或所成角的补角），
设正四面体ABCD的棱长为2，由BM=DE= ，OD= ，
∴AO= = ，∴MN= ，
∵O是点A在底面BCD内的射影，MN∥AO，∴MN⊥平面BCD，
∴cos∠BMN= = = ，
∴异面直线BM与AO所成角的余弦值为 ．
故选：B．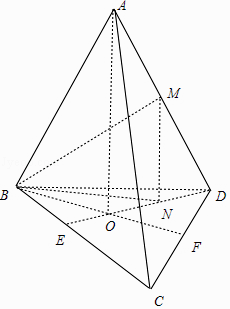

取BC中点E，DC中点F，连结DE、BF，则由题意得DE∩BF=O，取OD中点N，连结MN，则MN∥AO，从而∠BMN是异面直线BM与AO所成角（或所成角的补角），由此能求出异面直线BM与AO所成角的余弦值．