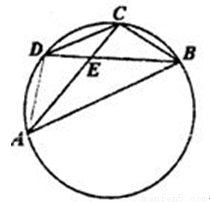
题目内容
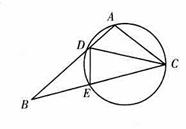
 如题一图,
如题一图,![]() 是圆内接四边形.
是圆内接四边形.![]() 与
与![]() 的交点为
的交点为![]() ,
,![]() 是弧
是弧![]() 上一点,连接
上一点,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,点
,点![]() 分别在
分别在![]() ,
,![]() 的延长线上,满足
的延长线上,满足![]() ,
,![]() ,求证:
,求证:![]() 四点共圆.
四点共圆.
[证] 由已知条件知
![]() .
.
又![]() ,
,
所以![]() ,
,
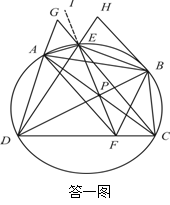 从而
从而![]() 四点共圆,此圆记为
四点共圆,此圆记为![]() .
.
同理可证:![]() 四点共圆,此圆记为
四点共圆,此圆记为![]() .
.
点![]() 在圆
在圆![]() ,
,![]() 内.延长
内.延长![]() 与圆
与圆![]() 相交于点
相交于点![]() ,则
,则
![]() ,
,
故![]() 四点共圆.
四点共圆.
所以![]() 在
在![]() 的外接圆上,故
的外接圆上,故![]() 在
在![]() 上.
上.
再用相交弦定理:
![]() ,
,
故![]() 四点共圆.
四点共圆.
解析:
解析见答案

练习册系列答案
相关题目
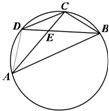 如图,在圆内接四边形ABCD中,对角线AC,BD相交于点E.已知
如图,在圆内接四边形ABCD中,对角线AC,BD相交于点E.已知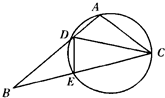 如图,四边形ACED是圆内接四边形,延长AD与CE的延长线交于点B,且AD=DE,AB=2AC.
如图,四边形ACED是圆内接四边形,延长AD与CE的延长线交于点B,且AD=DE,AB=2AC. 是圆内接四边形,延长
是圆内接四边形,延长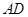 与的延长线
与的延长线 交于点
交于点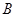 ,且
,且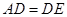 ,
, 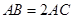 .
.
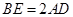 ;
;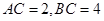 时,求
时,求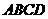 中,对角线
中,对角线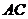 ,
,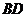 相交于点
相交于点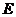 。已知
。已知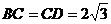 ,
,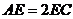 ,
,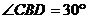 ,则
,则 _____________,
_____________,