题目内容
已知数列{an}中,a1=3,a2=5,Sn为其前n项和,且满足Sn+Sn-2=2Sn-1+2n-1(n≥3,n∈N*).(1)求数列{an}的通项公式;
(2)令bn=
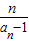 ,求数列{bn}的前n项和Tn;
,求数列{bn}的前n项和Tn;(3)若f(x)=2x-1,cn=
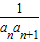 ,Qn=c1f(1)+c2f(2)+…+cnf(n),求证Qn<
,Qn=c1f(1)+c2f(2)+…+cnf(n),求证Qn< (n∈N*).
(n∈N*).
【答案】分析:(1)由Sn+Sn-2=2Sn-1+2n-1得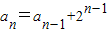 (n≥3,n∈N*),利用累加法可求得an,注意验证a1=3,a2=5的情形;
(n≥3,n∈N*),利用累加法可求得an,注意验证a1=3,a2=5的情形;
(2)由(1)易求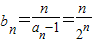 ,利用错位相减法可求得Tn;
,利用错位相减法可求得Tn;
(3)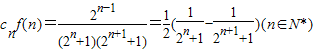 ,利用裂项相消法可求得Qn,然后适当放缩可证明不等式;
,利用裂项相消法可求得Qn,然后适当放缩可证明不等式;
解答:解:(1)由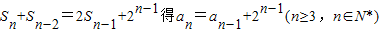 ,
,
∵a2=5,∴当n≥3时,an=a2+(a3-a2)+(a4-a3)+…+(an-an-1)=5+22+23+…+2n-1=2n+1,
经验证a1=3,a2=5也符合上式,
∴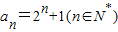 ;
;
(2)由(1)可得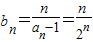 ,
,
∴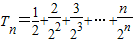 ①
①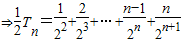 ②,
②,
①-②有: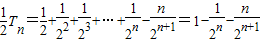 ,
,
∴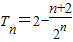 ;
;
(3)∵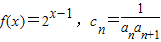 ,
,
∴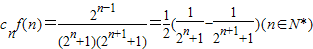 ,
,
∴Qn=c1f(1)+c2f(2)+…+cnf(n)
=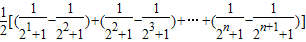
=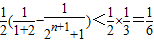 .
.
点评:本题考查数列与不等式的综合、错位相减法及裂项相消法对数列求和,考查学生综合运用知识解决问题的能力.
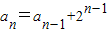 (n≥3,n∈N*),利用累加法可求得an,注意验证a1=3,a2=5的情形;
(n≥3,n∈N*),利用累加法可求得an,注意验证a1=3,a2=5的情形;(2)由(1)易求
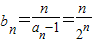 ,利用错位相减法可求得Tn;
,利用错位相减法可求得Tn;(3)
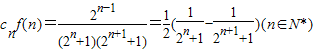 ,利用裂项相消法可求得Qn,然后适当放缩可证明不等式;
,利用裂项相消法可求得Qn,然后适当放缩可证明不等式;解答:解:(1)由
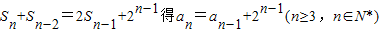 ,
,∵a2=5,∴当n≥3时,an=a2+(a3-a2)+(a4-a3)+…+(an-an-1)=5+22+23+…+2n-1=2n+1,
经验证a1=3,a2=5也符合上式,
∴
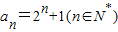 ;
;(2)由(1)可得
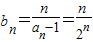 ,
,∴
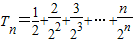 ①
①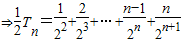 ②,
②,①-②有:
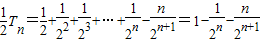 ,
,∴
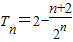 ;
;(3)∵
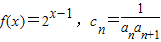 ,
,∴
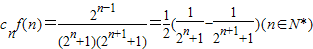 ,
,∴Qn=c1f(1)+c2f(2)+…+cnf(n)
=
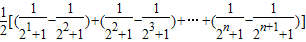
=
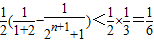 .
.点评:本题考查数列与不等式的综合、错位相减法及裂项相消法对数列求和,考查学生综合运用知识解决问题的能力.

练习册系列答案
相关题目
已知数列{an}中,a1=1,2nan+1=(n+1)an,则数列{an}的通项公式为( )
A、
| ||
B、
| ||
C、
| ||
D、
|