Question

【题目】已知圆心为的圆过点，且与直线相切于点。

（1）求圆的方程；

（2）已知点，且对于圆上任一点，线段上存在异于点的一点，使得（为常数），试判断使的面积等于4的点有几个，并说明理由。

Answer 1

【答案】（1）（2）使的面积等于4的点有2个

【解析】

（1）利用条件设圆的标准方程，由圆过点求t，确定圆方程.

（2）设，由确定阿波罗尼斯圆方程，与圆C为同一圆，可得，求出N点的坐标，建立ON方程，,再利用面积求点P到直线的距离，

判断与ON平行且距离为的两条直线与圆C的位置关系可得结论.

（1）依题意可设圆心坐标为，则半径为，

圆的方程可写成，

因为圆过点，∴，∴，

则圆的方程为。

（2）由题知，直线的方程为，设满足题意，

设，则，所以，

则，

因为上式对任意恒成立，所以，且，

解得或（舍去，与重合）。

所以点，则，直线方程为，

点到直线的距离，

若存在点使的面积等于4，则，

∴。

①当点在直线的上方时，点到直线的距离的取值范围为，

∵，

∴当点在直线的上方时，使的面积等于4的点有2个；

②当点在直线的下方时，点到直线的距离的取值范围为，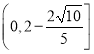

∵，

∴当点在直线的下方时，使的面积等于4的点有0个，

综上可知，使的面积等于4的点有2个。