题目内容
【题目】若数列![]() 满足n≥2时,
满足n≥2时,![]() ,则称数列
,则称数列![]() (n
(n![]() )为
)为![]() 的“L数列”.
的“L数列”.
(1)若![]() ,且
,且![]() 的“L数列”为
的“L数列”为![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,且
,且![]() 的“L数列”为递增数列,求k的取值范围;
的“L数列”为递增数列,求k的取值范围;
(3)若![]() ,其中p>1,记
,其中p>1,记![]() 的“L数列”的前n项和为
的“L数列”的前n项和为![]() ,试判断是否存在等差数列
,试判断是否存在等差数列![]() ,对任意n
,对任意n![]() ,都有
,都有![]() 成立,并证明你的结论.
成立,并证明你的结论.
【答案】(1)![]() ;(2)(1,+∞);(3)存在满足条件的等差数列
;(2)(1,+∞);(3)存在满足条件的等差数列![]() ,见解析
,见解析
【解析】
(1)由题意知![]() 即
即![]() ,利用累乘法即可求得通项公式;(2)由
,利用累乘法即可求得通项公式;(2)由![]() 可得
可得![]() ,设
,设![]() ,根据题意{bn}为递增数列,只需
,根据题意{bn}为递增数列,只需![]() -
-![]() >0恒成立即可求得满足题意的k值;(3)根据
>0恒成立即可求得满足题意的k值;(3)根据![]() 的通项公式求出
的通项公式求出![]() ,利用放缩法及等比数列的前n项和公式可得
,利用放缩法及等比数列的前n项和公式可得![]() ,再次利用
,再次利用![]() 放缩可得
放缩可得![]() ,设
,设![]() ,易证其为等差数列,结论成立.
,易证其为等差数列,结论成立.
(1)由题意知,![]() 即
即![]() ,
,
所以![]() ,
,
即数列![]() 的通项公式为
的通项公式为![]() .
.
(2)因为![]() ,且n≥2,n∈N*时,
,且n≥2,n∈N*时,![]() ,所以
,所以![]() ,
,
设![]() ,n∈N*,所以
,n∈N*,所以![]() 1-
1-![]() .
.
因为{bn}为递增数列,所以![]() 对n∈N*恒成立,
对n∈N*恒成立,
即![]() -
-![]() >0对
>0对![]() 恒成立.
恒成立.
因为![]() -
-![]() =
=![]() ,
,
所以![]() -
-![]() >0等价于
>0等价于![]() .
.
当0<k≤1时,因为n=1时,![]() ,不符合题意.
,不符合题意.
当k>1时,![]() ,所以
,所以![]() ,
,
综上,k的取值范围是![]() .
.
(3)存在满足条件的等差数列![]() ,证明如下:
,证明如下:
因为 ,k
,k![]() ,
,
所以![]() ,又因为
,又因为![]() ,所以
,所以![]() ,
,
所以![]() ,
,
即![]() ,因为
,因为![]() ,所以
,所以![]() ,
,
设![]() ,则
,则![]() ,且
,且![]() ,
,
所以存在等差数列![]() 满足题意.
满足题意.

【题目】我国新型冠状病毒肺炎疫情期间,以网络购物和网上服务所代表的新兴消费展现出了强大的生命力,新兴消费将成为我国消费增长的新动能.某市为了了解本地居民在2020年2月至3月两个月网络购物消费情况,在网上随机对1000人做了问卷调查,得如下频数分布表:
网购消费情况(元) |
|
|
|
|
|
频数 | 300 | 400 | 180 | 60 | 60 |
(1)作出这些数据的频率分布直方图,并估计本市居民此期间网络购物的消费平均值;
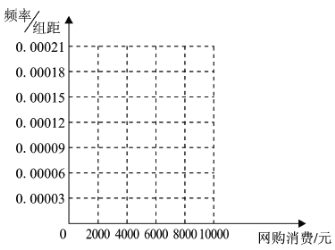
(2)在调查问卷中有一项是填写本人年龄,为研究网购金额和网购人年龄的关系,以网购金额是否超过4000元为标准进行分层抽样,从上述1000人中抽取200人,得到如下列联表,请将表补充完整并根据列联表判断,在此期间是否有95%的把握认为网购金额与网购人年龄有关.
网购不超过4000元 | 网购超过4000元 | 总计 | |
40岁以上 | 75 | 100 | |
40岁以下(含40岁) | |||
总计 | 200 |
参考公式和数据:![]() .(其中
.(其中![]() 为样本容量)
为样本容量)
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |