题目内容
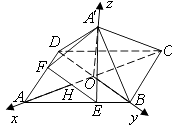
【题目】如图,已知正方形ABCD的边长为6,点E,F分别在边AB,AD上,AE=AF=4,现将△AEF沿线段EF折起到△A′EF位置,使得A′C=2 ![]() .
. 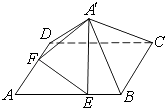
(1)求五棱锥A′﹣BCDFE的体积;
(2)求平面A′EF与平面A′BC的夹角.
【答案】
(1)解:连接AC,设AC∩EF=H,
由ABCD是正方形,AE=AF=4,
得H是EF的中点,
且EF⊥AH,EF⊥CH,
从而有A′H⊥EF,CH⊥EF,
∴EF⊥平面A′HC,
从而平面A′HC⊥平面ABCD,
过点A′作A′O垂直HC且与HC相交于点O,
则A′O⊥平面ABCD.
∵正方形ABCD的边长为6,AE=AF=4,
得到: ![]() ,CH=4
,CH=4 ![]() ,
,
∴cos∠A′HC= ![]() =
= ![]() ,
,
∴HO= ![]() ,
, ![]() ,
,
∴五棱锥A′﹣BCDFE的体积V= ![]() =
= ![]()
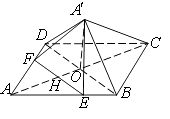
(2)解:由(1)得A′O⊥平面ABCD,且CO=3 ![]() ,即点O是AC,BD的交点,
,即点O是AC,BD的交点,
如图以点O为原点,OA,OB,OA′所在直线分别为x轴,y轴,z轴,
建立空间直角坐标系,
则由题意知 ![]() ,B(0,3
,B(0,3 ![]() ,0),C(﹣3
,0),C(﹣3 ![]() ,0,0),D(0,﹣3
,0,0),D(0,﹣3 ![]() ,0),
,0),
E( ![]() ,2
,2 ![]() ,0),F(
,0),F( ![]() ,﹣2
,﹣2 ![]() ,0),
,0), ![]() ,
,
∴ ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
设平面A′EF的法向量为 ![]() =(x,y,z),
=(x,y,z),
则 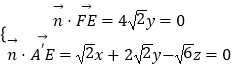 ,
,
取x= ![]() ,得
,得 ![]() ,
,
设平面A′BC的法向量 ![]() ,
,
则 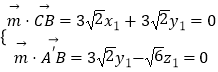 ,
,
令y1=1,得 ![]() =(﹣1,1,
=(﹣1,1, ![]() ),
),
∴cos< ![]() >=0,即平面A′EF与平面A′BC夹角是
>=0,即平面A′EF与平面A′BC夹角是 ![]()
【解析】(1)连接AC,设AC∩EF=H,由已知条件推导出平面A′HC⊥平面ABCD,过点A′作A′O垂直HC且与HC相交于点O,则A′O⊥平面ABCD,由此能求出五棱锥A′﹣BCDFE的体积.(2)由(1)得A′O⊥平面ABCD,且CO=3 ![]() ,即点O是AC,BD的交点,以点O为原点,OA,OB,OA′所在直线分别为x轴,y轴,z轴,建立空间直角坐标系,利用向量法能求出平面A′EF与平面A′BC夹角.
,即点O是AC,BD的交点,以点O为原点,OA,OB,OA′所在直线分别为x轴,y轴,z轴,建立空间直角坐标系,利用向量法能求出平面A′EF与平面A′BC夹角.

【题目】为考察高中生的性别与是否喜欢数学课程之间的关系,在某城市的某校高中生中,从男生中随机抽取了70人,从女生中随机抽取了50人,男生中喜欢数学课程的占![]() ,女生中喜欢数学课程的占
,女生中喜欢数学课程的占![]() ,得到如下列联表.
,得到如下列联表.
喜欢数学课程 | 不喜欢数学课程 | 合计 | |
男生 | |||
女生 | |||
合计 |
(1)请将列联表补充完整;试判断能否有90%的把握认为喜欢数学课程与否与性别有关;
(2)从不喜欢数学课程的学生中采用分层抽样的方法,随机抽取6人,现从6人中随机抽取2人,求抽取的学生中至少有1名是女生的概率..
附:![]() ,其中
,其中![]() .
.
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |