Question

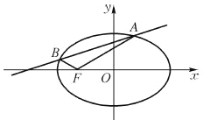
【题目】如图，在多面体中，△是等边三角形，△是等腰直角三角形，，平面⊥平面，⊥平面，点为的中点，连接．

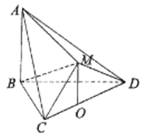
（1）求证：平面；

（2）若，求三棱锥的体积．

Answer 1

【答案】（1）证明见解析；（2）.

【解析】

试题分析：（1）因为为等腰直角三角形，且为中点，所以，又因为平面平面，且交线为，根据面面垂直的性质定理可得平面，又因为平面，根据垂直于同一平面的两条直线平行得，于是根据线面平行判定定理可证平面；（2）连接，由（1）知平面，点到平面的距离等于点到平面的距离，因此，由于地面是边长为的等边三角形，所以其面积为，则，根据已知⊥平面，所以三棱锥，所以.

试题解析：（1）证明：∵△是等腰直角三角形，，点为的中点，

∴⊥．

∵平面⊥平面，平面平面，平面，

∴⊥平面，

∵⊥平面，

∴，

∵平面，平面，

∴平面．

（2）由（1）知平面，

∵点到平面的距离等于点到平面的距离．

∵，△是等边三角形，

∴，，

连接，则⊥，，

，

∴三棱锥的体积为．