题目内容
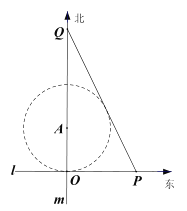
【题目】如图,某市有一条东西走向的公路![]() ,现欲经过公路
,现欲经过公路![]() 上的
上的![]() 处铺设一条南北走向的公路
处铺设一条南北走向的公路![]() .在施工过程中发现在
.在施工过程中发现在![]() 处的正北1百米的
处的正北1百米的![]() 处有一汉代古迹.为了保护古迹,该市决定以
处有一汉代古迹.为了保护古迹,该市决定以![]() 为圆心, 1百米为半径设立一个圆形保护区.为了连通公路
为圆心, 1百米为半径设立一个圆形保护区.为了连通公路![]() ,欲再新建一条公路
,欲再新建一条公路![]() ,点
,点 ![]() 分别在公路
分别在公路![]() 上,且求
上,且求![]() 与圆
与圆![]() 相切.
相切.
(1)当![]() 距
距![]() 处2百米时,求
处2百米时,求![]() 的长;
的长;
(2)当公路![]() 长最短时,求
长最短时,求![]() 的长.
的长.
【答案】(1)当![]() 距
距![]() 处2百米时,
处2百米时, ![]() 的长为
的长为![]() 百米;(2)当公路
百米;(2)当公路![]() 长最短时,
长最短时, ![]() 的长为
的长为![]() 百米.
百米.
【解析】试题分析:题目中涉及到直线与圆相切的条件,一般在平面直角坐标系中研究,所以先建立合适的坐标系;(1)已知点![]() ,则设直线
,则设直线![]() 的方程,可设截距(或点斜式),利用圆心到直线的距离等于半径,求得
的方程,可设截距(或点斜式),利用圆心到直线的距离等于半径,求得![]() 的坐标,从而得到
的坐标,从而得到![]() 的长;(2)研究
的长;(2)研究![]() 长的最小值,则需要建立目标函数,选择合适的变量,本小题依然可以设直线的两个截距,则容易表示出的
长的最小值,则需要建立目标函数,选择合适的变量,本小题依然可以设直线的两个截距,则容易表示出的![]() 长和直线方程,由相切再得到两截距间的关系,消元后则得到一个一元的函数,再利用导数研究它的最小值;
长和直线方程,由相切再得到两截距间的关系,消元后则得到一个一元的函数,再利用导数研究它的最小值;
试题解析:
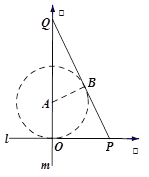
以![]() 为原点,直线
为原点,直线![]() 、
、![]() 分别为
分别为![]() 轴建立平面直角坐标系.
轴建立平面直角坐标系.
设![]() 与圆
与圆![]() 相切于点
相切于点![]() ,连结
,连结![]() ,以
,以![]() 百米为单位长度,则圆
百米为单位长度,则圆![]() 的方程为
的方程为![]() ,
,
(1)由题意可设直线![]() 的方程为
的方程为![]() ,即
,即![]() ,
, ![]() ,
,
∵![]() 与圆
与圆![]() 相切,∴
相切,∴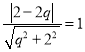 ,解得
,解得![]() ,
,
故当![]() 距
距![]() 处
处![]() 百米时,
百米时, ![]() 的长为
的长为![]() 百米.
百米.
(2)设直线![]() 的方程为
的方程为![]() ,即
,即![]() ,
, ![]() ,
,
∵![]() 与圆
与圆![]() 相切,∴
相切,∴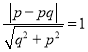 ,化简得
,化简得![]() ,则
,则![]() ,
,
令![]() ,∴
,∴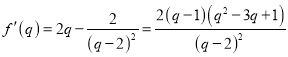
![]() ,
,
当![]() 时,
时, ![]() ,即
,即![]() 在
在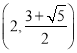 上单调递减;
上单调递减;
当![]() 时,
时, ![]() ,即
,即![]() 在
在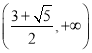 上单调递增,
上单调递增,
∴![]() 在
在![]() 时取得最小值,故当公路
时取得最小值,故当公路![]() 长最短时,
长最短时, ![]() 的长为
的长为![]() 百米.
百米.
答:(1)当![]() 距
距![]() 处
处![]() 百米时,
百米时, ![]() 的长为
的长为![]() 百米;(2)当公路
百米;(2)当公路![]() 长最短时,
长最短时, ![]() 的
的
长为![]() 百米.
百米.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目