题目内容
曲线y=cos(2x-
)的对称中心不可能是( )
| π |
| 6 |
A、(-
| ||
B、(-
| ||
C、(
| ||
D、(-
|
分析:由2x-
=kπ+
(k∈Z)得:x=
+
(k∈Z),对k赋值-4,-3,-2,0等值,分析判断即可.
| π |
| 6 |
| π |
| 2 |
| kπ |
| 2 |
| π |
| 3 |
解答:解:由2x-
=kπ+
(k∈Z)得:x=
+
(k∈Z),
当k=-4时,(-
,0)为其对称中心,故B符合题意;
当k=-3时,(-
,0)为其对称中心,故A不符合题意;
当k=-2时,(-
,0)为其对称中心,故D符合题意;
当k=0时,(
,0)为其对称中心,故C符合题意;
综上所述,曲线y=cos(2x-
)的对称中心不可能是(-
,0),
故选:A.
| π |
| 6 |
| π |
| 2 |
| kπ |
| 2 |
| π |
| 3 |
当k=-4时,(-
| 5π |
| 3 |
当k=-3时,(-
| 7π |
| 6 |
当k=-2时,(-
| 2π |
| 3 |
当k=0时,(
| π |
| 3 |
综上所述,曲线y=cos(2x-
| π |
| 6 |
| 5π |
| 6 |
故选:A.
点评:本题考查余弦函数的对称轴,考查赋值法,属于中档题.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
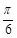 )的图像可由曲线y=1+cos2x向左平移
)的图像可由曲线y=1+cos2x向左平移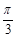 个单位得到;②函数y=sin(x+
个单位得到;②函数y=sin(x+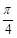 )+cos(x+
)+cos(x+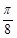 是曲线y=sin(2x+
是曲线y=sin(2x+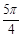 )的一条对称轴;④函数y=2sin2(x+
)的一条对称轴;④函数y=2sin2(x+