题目内容
正六棱锥的高为3，底面最长的对角线为4
，则其外接球的体积是 ．
| 3 |
分析：根据条件求出正六棱锥的底面边长，根据条件建立方程求出外接球的半径，即可求球的体积．
解答：解：∵正六棱锥的高为3，底面最长的对角线为4
，
∴PA=3，AB=2
，
根据正六棱锥的对称性可知球心O在高PA上，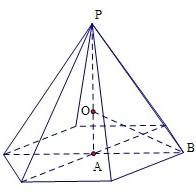
设半径为R，
则OA=PA-R=3-R，
∴在直角三角形OAB中，
OB2=OA2+AB2，
即R2=(3-R)2+(2
)2，
∴R2=9-6R+R2+12，
即R=
=
，
∴其外接球的体积是
×π×(
)3=
π，
故答案为：
π．
| 3 |
∴PA=3，AB=2
| 3 |
根据正六棱锥的对称性可知球心O在高PA上，
设半径为R，
则OA=PA-R=3-R，
∴在直角三角形OAB中，
OB2=OA2+AB2，
即R2=(3-R)2+(2
| 3 |
∴R2=9-6R+R2+12，
即R=
| 21 |
| 6 |
| 7 |
| 2 |
∴其外接球的体积是
| 4 |
| 3 |
| 7 |
| 2 |
| 343 |
| 6 |
故答案为：
| 343 |
| 6 |
点评：本题主要考查球的体积的计算，根据正六棱锥对称性建立方程，求出球的半径是解决本题的关键．
练习册系列答案
科学实验活动册系列答案
相关题目