题目内容
在锐角△ABC中，角A，B，C所对的边分别为a，b，c，已知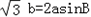
．
（1）求角A的大小；
（2）若a=6，求b+c的取值范围．
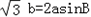．（1）求角A的大小；
（2）若a=6，求b+c的取值范围．
解：（1）由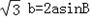
得：
，
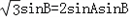又sinB≠0，
∴
，
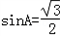由锐角△ABC得：A=60°；
（2）∵a=6，A=60°，设三角形外接圆的半径为R，
∴根据正弦定理得：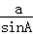
=
=
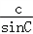=2R，
又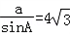
，
∴2R=4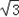
，
∴b=4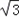
sinB，c=4
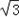sinC，
又A=60°，
∴B+C=120°，
即C=120°﹣B，
∴
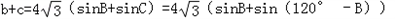
=4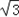
（sinB+sin120°cosB﹣cos120°sinB）
=4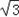
（sinB+
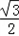cosB+
sinB）
=6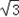
sinB+6cosB
=12（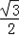
sinB+
cosB）
=12sin（B+30°），
∵△ABC为锐角三角形，
∴B∈（30°，90°），
∴B+30°∈（60°，120°）
∴
，
∴
．
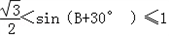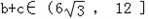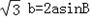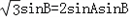得：，又sinB≠0，
∴
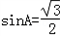，由锐角△ABC得：A=60°；
（2）∵a=6，A=60°，设三角形外接圆的半径为R，
∴根据正弦定理得：
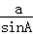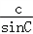===2R，又
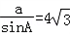，∴2R=4
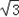，∴b=4
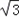sinB，c=4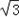sinC，又A=60°，
∴B+C=120°，
即C=120°﹣B，
∴
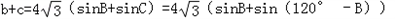
=4
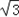（sinB+sin120°cosB﹣cos120°sinB）=4
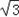（sin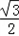B+cosB+sinB）=6
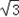sinB+6cosB=12（
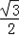sinB+cosB）=12sin（B+30°），
∵△ABC为锐角三角形，
∴B∈（30°，90°），
∴B+30°∈（60°，120°）
∴
，∴
．
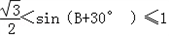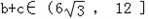练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
点睛新教材全能解读系列答案
相关题目