题目内容
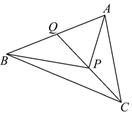
如图所示,P是△ABC内一点,且满足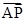 +
+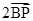 +
+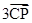 =
=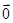 ,设Q为CP延长线与AB的交点,求证:
,设Q为CP延长线与AB的交点,求证: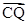 =
=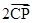 .
.
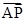 +
+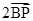 +
+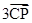 =
=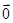 ,设Q为CP延长线与AB的交点,求证:
,设Q为CP延长线与AB的交点,求证: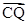 =
=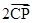 .
.
证明见解析
试题分析:
解题思路:先将
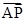 +
+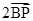 +
+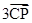 =
=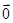 转化为与
转化为与 有关的向量,再利用
有关的向量,再利用 与
与 三点共线进行证明.
三点共线进行证明.规律总结:涉及平面向量在平面几何中证明问题,一要合理选择基向量,二要合理利用三点共线或向量共线进行线性表示.
试题解析:∵
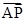 =
= ,
, =
= , ∴
, ∴ =
=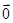 ,
,∴
 =
=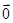 ,
,又∵A,B,Q三点共线,C,P,Q三点共线,故可设
 =
= ,
, =μ
=μ ,
,∴
 =
=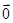 ,
,∴
 =
=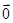 .
.而
 ,
, 为不共线向量,
为不共线向量,∴
 .
.∴λ=-2,μ=-1.
∴
 =
= =
= .故
.故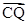 =
= =
=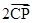 .
. 
练习册系列答案
相关题目
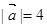 ,
,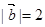 ,且
,且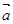 与
与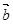 夹角为
夹角为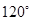 ,求
,求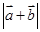 ;
; 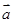 与
与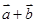 的夹角.
的夹角.
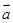 、
、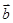 是非零向量,它们之间有如下一种运算:
是非零向量,它们之间有如下一种运算: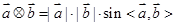 ,其中
,其中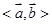 表示
表示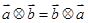 ;
;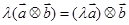 ;
;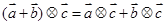 ;
;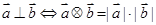 ;
;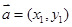 ,
,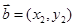 ,则
,则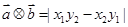 .
.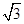 ,|
,|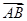 +
+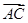 |=|
|=|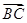 |,则
|,则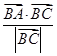 =________.
=________. ,
, ,
, 为坐标原点,点C在∠AOB内,且
为坐标原点,点C在∠AOB内,且 ,设
,设 ,则
,则 的值为( )
的值为( )



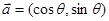 ,向量
,向量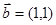 ,则
,则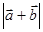 的最大值是 。
的最大值是 。