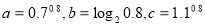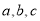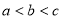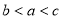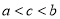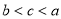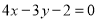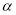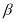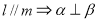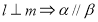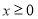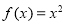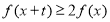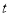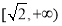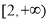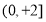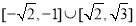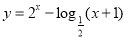题目内容
函数 的定义域为
的定义域为 (a为实数),
(a为实数),
(1)当 时,求函数
时,求函数 的值域。
的值域。
(2)若函数 在定义域上是减函数,求a的取值范围
在定义域上是减函数,求a的取值范围
(3)求函数 在
在 上的最大值及最小值。
上的最大值及最小值。
(1)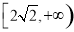 (2)
(2)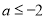 (3)无最大值,最小值为
(3)无最大值,最小值为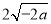
【解析】
试题分析:(1)当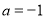 时
时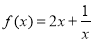 ,符合基本不等式“一正,二定,三相等”的条件,固可用基本不等式求函数最值(2)利用函数单调性的定义求出
,符合基本不等式“一正,二定,三相等”的条件,固可用基本不等式求函数最值(2)利用函数单调性的定义求出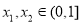 时只要
时只要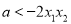 即可,转化为恒成立问题。利用
即可,转化为恒成立问题。利用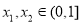 求出
求出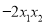 的范围即可求得
的范围即可求得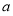 范围。(3)分类讨论
范围。(3)分类讨论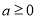 时函数
时函数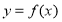 在
在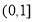 上单调递增,无最小值。由(2)得当
上单调递增,无最小值。由(2)得当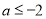 时,
时,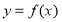 在
在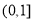 上单调递减,无最大值,当
上单调递减,无最大值,当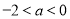 时,利用对勾函数分析其单调性求最值。具体过程详见解析
时,利用对勾函数分析其单调性求最值。具体过程详见解析
试题解析:(1)当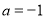 时,
时,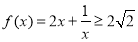 ,当且仅当
,当且仅当 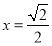 时取
时取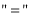 , 所以值域为
, 所以值域为 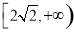
(2)若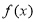 在定义域上是减函数,则任取
在定义域上是减函数,则任取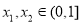 且
且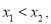 都有
都有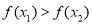 成立,即
成立,即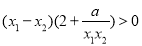 只要
只要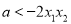 即可 由
即可 由
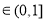 且
且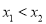
故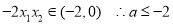
(3)当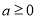 时,函数
时,函数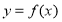 在
在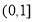 上单调递增,无最小值,当
上单调递增,无最小值,当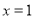 时,
时,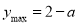
由(2)得当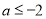 时,
时,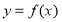 在
在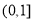 上单调递减,无最大值,当
上单调递减,无最大值,当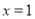 时,
时,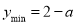
当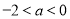 时,
时, 此时函数
此时函数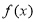 在
在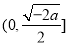 上单调递减,
上单调递减,
在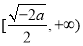 上单调递增,无最大值,
上单调递增,无最大值, 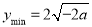
考点:(1)函数的单调性(2)利用函数单调性求最值问题

练习册系列答案
 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目