Question

已知函数=ax³+bx²+cx在点x₀处取得极大值5,其导函数y=

的图象经过点(1,0),(2,0).如图所示.求:

(1)x₀的值;

(2)a、b、c的值.

Answer 1

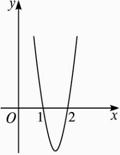
(1)解：由图象可知,在(-∞,1)上>0,在(1,2)上<0.在(2,+∞)上>0.

故在(-∞,1),(2,+∞)上递增,在(1,2)上递减.

因此在x=1处取得极大值,所以x₀=1.

(2)解法一：=3ax²+2bx+c,

由f′(1)=0,f′(2)=0,f(1)=5,

得解得a=2,b=-9,c=12.

解法二：设=m(x-1)(x-2)=mx²-3mx+2m,

又=3ax²+2bx+c,

所以a=,b=-m,c=2m,

= x³-mx²+2mx.

由f(1)=5,

即-m+2m=5,

得m=6,

所以a=2,b=-9,c=12.